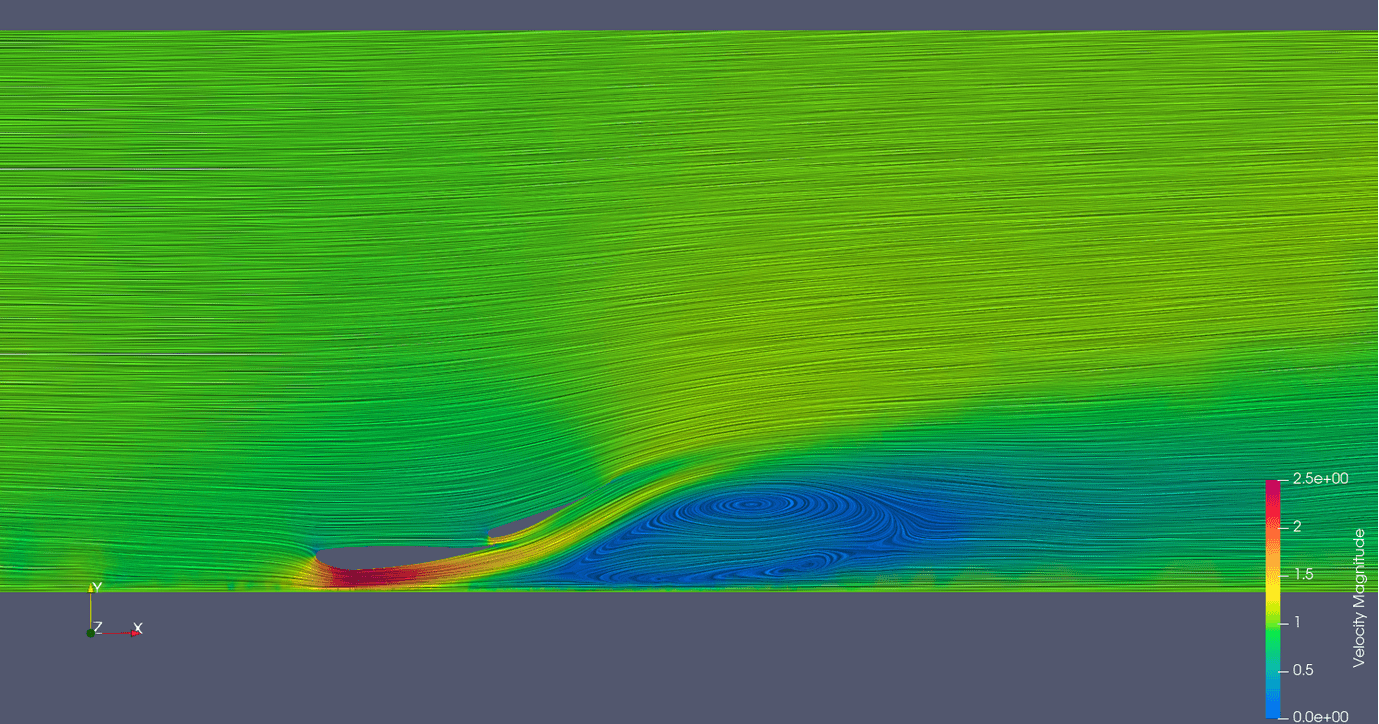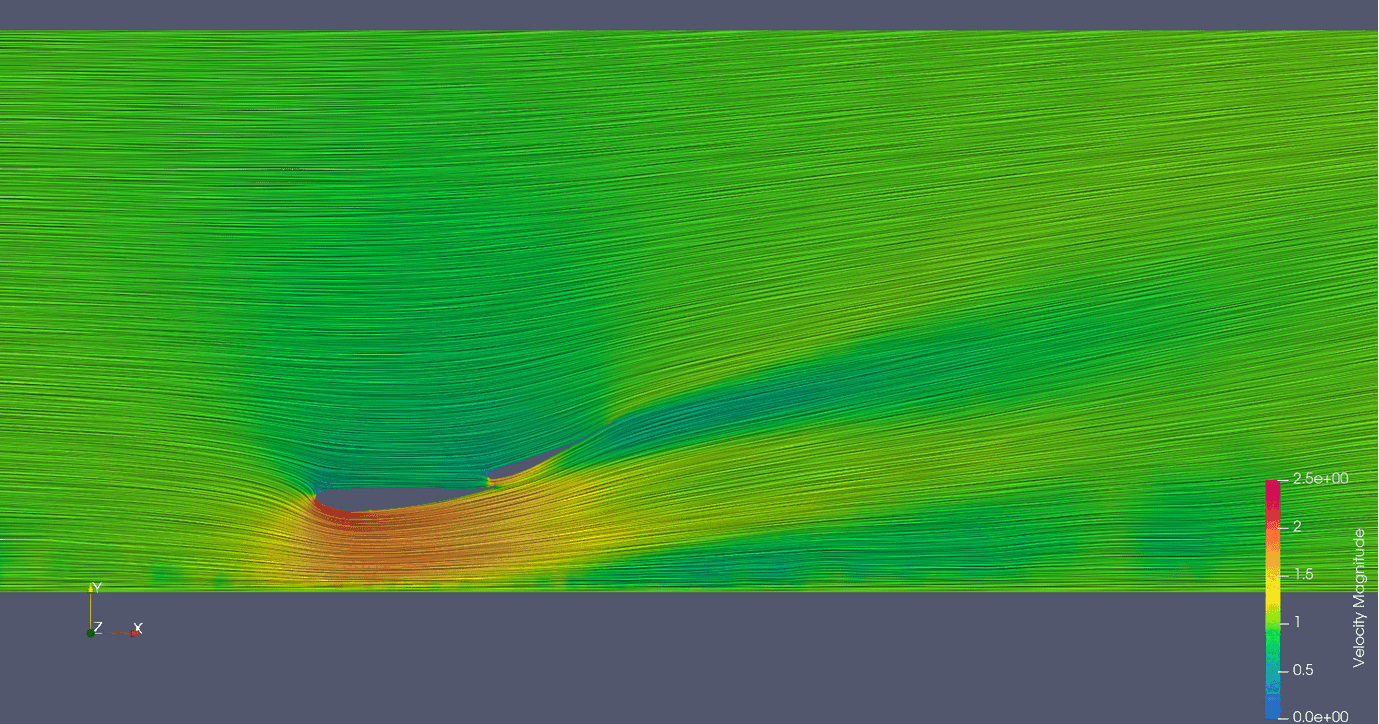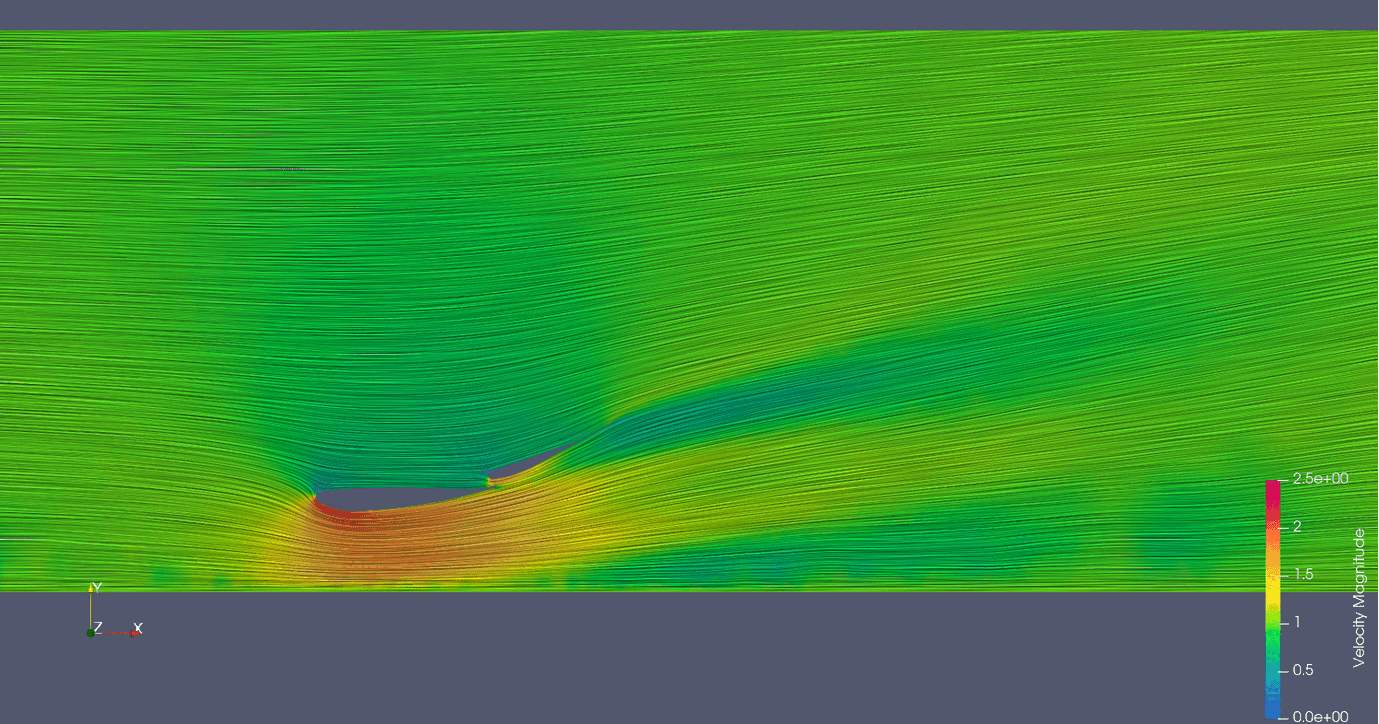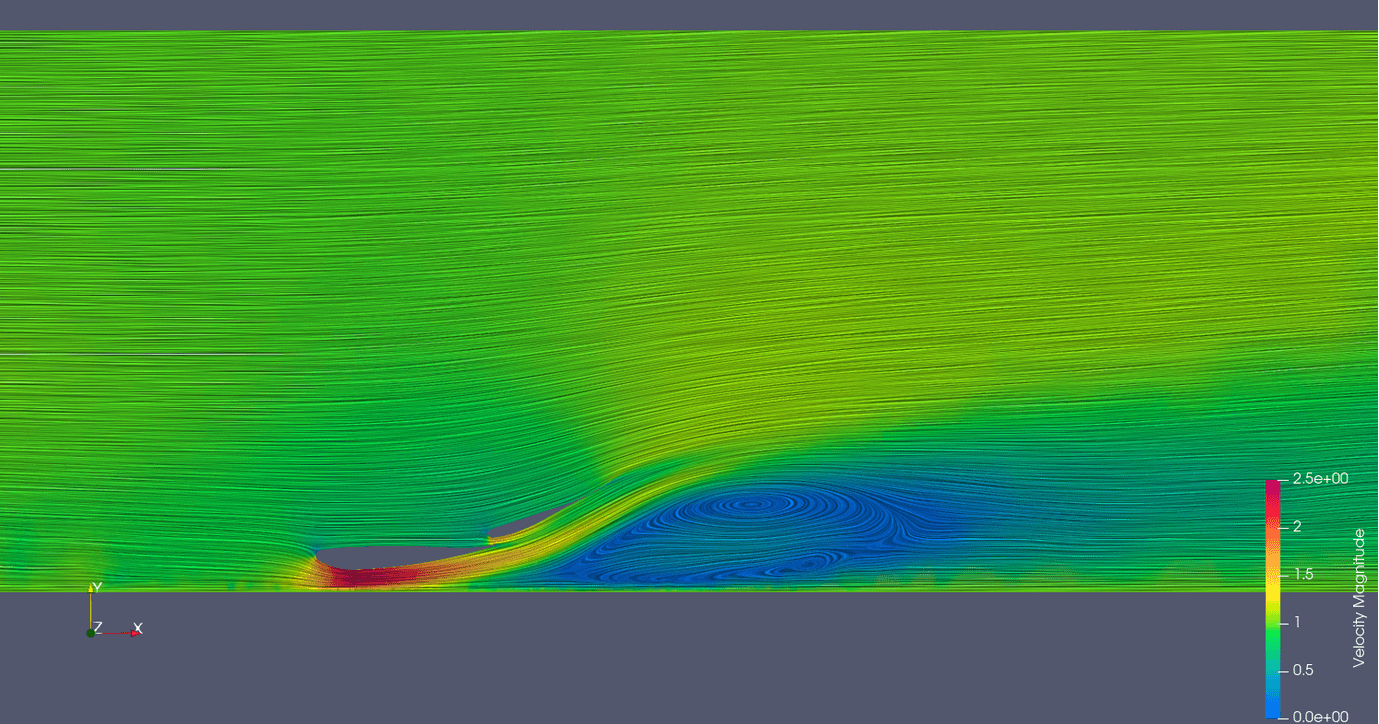
Links
- Download Thesis PDF
- Download Thesis PDF - UnB Library
- Download CONEM24 Paper PDF
- DOI: 10.26678/abcm.conem2024.con24-0426
Title (English)
Open Source Numerical Simulations of Turbulent Flow over Downforce Generating Multielement Wings in Ground Effect
Abstract (English)
This work tries to establish and validate a complete cycle of computational fluid dynamics simulations using open-source tools. The main objective is to demonstrate the feasibility and reliability of using open-source tools to simulate complex fluid dynamic phenomena. To achieve this goal, the simulation cycle is established using the following programs: SALOME for mesh generation and pre-processing, SU2 for numerical calculations, and Paraview for results and data visualization. The chosen geometry for validating this simulation cycle is the geometry of the experiments in the doctoral thesis by Zerihan (2001), which consists of a Formula 1 car's front wing inside a wind tunnel. The case was modeled in CAD software, three dimensional meshes were generated, and simulations were conducted to compare the values of the dimensionless aerodynamic coefficients obtained with the literature. The methodology employed during the simulation cycle is described in detail, with justifications for decisions made and observations on the workflow in the programs used. The results of this work demonstrate a good capability to capture complex aerodynamic phenomena and establish a reliable approach for solving problems in computational fluid dynamics.
SU2 Configuration Files
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% %
% SU2 configuration file %
% Case description: Tyrrell 026 Front Wing in Wind Tunnel - h17mm___________ %
% Author: Matheus Ribeiro Vidal______________________________________________ %
% Institution: Universidade de Brasilia______________________________________ %
% Date: 13/06/2023 %
% File Version 7.3.1 "Blackbird" %
% %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% ------------- DIRECT, ADJOINT, AND LINEARIZED PROBLEM DEFINITION ------------%
%
% Solver type (EULER, NAVIER_STOKES, RANS,
% INC_EULER, INC_NAVIER_STOKES, INC_RANS,
% NEMO_EULER, NEMO_NAVIER_STOKES,
% FEM_EULER, FEM_NAVIER_STOKES, FEM_RANS, FEM_LES,
% HEAT_EQUATION_FVM, ELASTICITY)
SOLVER= INC_RANS
%
% Specify turbulence model (NONE, SA, SA_NEG, SST, SA_E, SA_COMP, SA_E_COMP, SST_SUST)
KIND_TURB_MODEL= SST
%
% Mathematical problem (DIRECT, CONTINUOUS_ADJOINT, DISCRETE_ADJOINT)
% Defaults to DISCRETE_ADJOINT for the SU2_*_AD codes, and to DIRECT otherwise.
MATH_PROBLEM= DIRECT
%
% System of measurements (SI, US)
% International system of units (SI): ( meters, kilograms, Kelvins,
% Newtons = kg m/s^2, Pascals = N/m^2,
% Density = kg/m^3, Speed = m/s,
% Equiv. Area = m^2 )
SYSTEM_MEASUREMENTS= SI
%
%
% ------------------------------- SOLVER CONTROL ------------------------------%
%
% Number of iterations for single-zone problems
ITER= 1
%
% Maximum number of inner iterations
INNER_ITER= 15000
%
% Maximum number of outer iterations (only for multizone problems)
OUTER_ITER= 1
%
% Maximum number of time iterations
TIME_ITER= 1
%
% Convergence field
CONV_FIELD= PRESSURE
%
% Min value of the residual (log10 of the residual)
CONV_RESIDUAL_MINVAL= -8
%
% Start convergence criteria at iteration number
CONV_STARTITER= 10
%
% Number of elements to apply the criteria
CONV_CAUCHY_ELEMS= 100
%
% Epsilon to control the series convergence
CONV_CAUCHY_EPS= 1E-10
%
% Iteration number to begin unsteady restarts
RESTART_ITER= 0
%
%% Time convergence monitoring
WINDOW_CAUCHY_CRIT = YES
%
% List of time convergence fields
CONV_WINDOW_FIELD = (TAVG_DRAG, TAVG_LIFT)
%
% Time Convergence Monitoring starts at Iteration WINDOW_START_ITER + CONV_WINDOW_STARTITER
CONV_WINDOW_STARTITER = 0
%
% Epsilon to control the series convergence
CONV_WINDOW_CAUCHY_EPS = 1E-3
%
% Number of elements to apply the criteria
CONV_WINDOW_CAUCHY_ELEMS = 10
%
% ------------------------- TIME-DEPENDENT SIMULATION -------------------------------%
%
% Time domain simulation
TIME_DOMAIN= NO
%
% Unsteady simulation (NO, TIME_STEPPING, DUAL_TIME_STEPPING-1ST_ORDER,
% DUAL_TIME_STEPPING-2ND_ORDER, HARMONIC_BALANCE)
TIME_MARCHING= NO
%
% Time Step for dual time stepping simulations (s) -- Only used when UNST_CFL_NUMBER = 0.0
% For the DG-FEM solver it is used as a synchronization time when UNST_CFL_NUMBER != 0.0
TIME_STEP= 0.00001
%
% Total Physical Time for dual time stepping simulations (s)
MAX_TIME= 2.0
%
% Unsteady Courant-Friedrichs-Lewy number of the finest grid
UNST_CFL_NUMBER= 1.0
%
%% Windowed output time averaging
% Time iteration to start the windowed time average in a direct run
WINDOW_START_ITER = 500
%
% Window used for reverse sweep and direct run. Options (SQUARE, HANN, HANN_SQUARE, BUMP) Square is default.
WINDOW_FUNCTION = SQUARE
%
% ------------------------------- DES Parameters ------------------------------%
%
% Specify Hybrid RANS/LES model (SA_DES, SA_DDES, SA_ZDES, SA_EDDES)
HYBRID_RANSLES= SA_DDES
%
% DES Constant (0.65)
DES_CONST= 0.65
%
% ---------------- INCOMPRESSIBLE FLOW CONDITION DEFINITION -------------------%
%
% Density model within the incompressible flow solver.
% Options are CONSTANT (default), BOUSSINESQ, or VARIABLE. If VARIABLE,
% an appropriate fluid model must be selected.
INC_DENSITY_MODEL= CONSTANT
%
% Solve the energy equation in the incompressible flow solver
INC_ENERGY_EQUATION = NO
%
% Initial density for incompressible flows
% (1.2886 kg/m^3 by default (air), 998.2 Kg/m^3 (water))
INC_DENSITY_INIT= 1.2886
%
% Initial velocity for incompressible flows (1.0,0,0 m/s by default)
INC_VELOCITY_INIT= ( 30.0, 0.0, 0.0 )
%
% Initial temperature for incompressible flows that include the
% energy equation (288.15 K by default). Value is ignored if
% INC_ENERGY_EQUATION is false.
INC_TEMPERATURE_INIT= 288.15
%
% Non-dimensionalization scheme for incompressible flows. Options are
% INITIAL_VALUES (default), REFERENCE_VALUES, or DIMENSIONAL.
% INC_*_REF values are ignored unless REFERENCE_VALUES is chosen.
INC_NONDIM= INITIAL_VALUES
%
% Reference density for incompressible flows (1.0 kg/m^3 by default)
INC_DENSITY_REF= 1.0
%
% Reference velocity for incompressible flows (1.0 m/s by default)
INC_VELOCITY_REF= 1.0
%
% Reference temperature for incompressible flows that include the
% energy equation (1.0 K by default)
INC_TEMPERATURE_REF = 1.0
%
% List of inlet types for incompressible flows. List length must
% match number of inlet markers. Options: VELOCITY_INLET, PRESSURE_INLET.
INC_INLET_TYPE= VELOCITY_INLET
%
% Damping coefficient for iterative updates at pressure inlets. (0.1 by default)
INC_INLET_DAMPING= 0.1
%
% List of outlet types for incompressible flows. List length must
% match number of outlet markers. Options: PRESSURE_OUTLET, MASS_FLOW_OUTLET
INC_OUTLET_TYPE= PRESSURE_OUTLET
%
% Damping coefficient for iterative updates at mass flow outlets. (0.1 by default)
INC_OUTLET_DAMPING= 0.1
%
% Epsilon^2 multipier in Beta calculation for incompressible preconditioner.
BETA_FACTOR= 4.1
%
% ---------------------- REFERENCE VALUE DEFINITION ---------------------------%
%
% Reference origin for moment computation (m or in) % Atualmente em um quarto de Asa
REF_ORIGIN_MOMENT_X = 0.00
REF_ORIGIN_MOMENT_Y = 0.00
REF_ORIGIN_MOMENT_Z = 0.00
%
% Reference length for moment non-dimensional coefficients (m or in)
REF_LENGTH= 0.380
%
% Reference area for non-dimensional force coefficients (0 implies automatic
% calculation) (m^2 or in^2)
REF_AREA= 0.405
%
% Aircraft semi-span (0 implies automatic calculation) (m or in)
SEMI_SPAN= 0.0
%
% --------------------------- VISCOSITY MODEL ---------------------------------%
%
% Viscosity model (SUTHERLAND, CONSTANT_VISCOSITY, POLYNOMIAL_VISCOSITY).
VISCOSITY_MODEL= CONSTANT_VISCOSITY
% Molecular Viscosity that would be constant (1.716E-5 by default)
MU_CONSTANT= 1.716E-5
%
% Sutherland Viscosity Ref (1.716E-5 default value for AIR SI)
MU_REF= 1.716E-5
%
% Sutherland Temperature Ref (273.15 K default value for AIR SI)
MU_T_REF= 273.15
%
% Sutherland constant (110.4 default value for AIR SI)
SUTHERLAND_CONSTANT= 110.4
%
% Temperature polynomial coefficients (up to quartic) for viscosity.
% Format -> Mu(T) : b0 + b1*T + b2*T^2 + b3*T^3 + b4*T^4
MU_POLYCOEFFS= (0.0, 0.0, 0.0, 0.0, 0.0)
%
% ----------------------- DYNAMIC MESH DEFINITION -----------------------------%
%
% Type of dynamic surface movement (NONE, DEFORMING, MOVING_WALL,
% AEROELASTIC, AEROELASTIC_RIGID_MOTION EXTERNAL, EXTERNAL_ROTATION)
SURFACE_MOVEMENT= MOVING_WALL
%
% Moving wall boundary marker(s) (NONE = no marker, ignored for RIGID_MOTION)
MARKER_MOVING= ( ground )
%
% Coordinates of the motion origin
SURFACE_MOTION_ORIGIN= -4 0.0 0.0
%
% Translational velocity (m/s or ft/s) in the x, y, & z directions
SURFACE_TRANSLATION_RATE = 30.0 0.0 0.0
%
%
% Move Motion Origin for marker moving (1 or 0)
MOVE_MOTION_ORIGIN = 0
%
% -------------------- BOUNDARY CONDITION DEFINITION --------------------------%
%
% Euler wall boundary marker(s) (NONE = no marker)
% Implementation identical to MARKER_SYM.
MARKER_EULER= ( wall )
%
% Navier-Stokes (no-slip), constant heat flux wall marker(s) (NONE = no marker)
% Format: ( marker name, constant heat flux (J/m^2), ... )
MARKER_HEATFLUX= ( wing, 0, ground, 0)
%
% Far-field boundary marker(s) (NONE = no marker)
MARKER_FAR= ( inlet, outlet )
%
% Inlet boundary type (TOTAL_CONDITIONS, MASS_FLOW)
%
%INLET_TYPE= TOTAL_CONDITIONS
%
% Inlet boundary marker(s) with the following formats (NONE = no marker)
% Total Conditions: (inlet marker, total temp, total pressure, flow_direction_x,
% flow_direction_y, flow_direction_z, ... ) where flow_direction is
% a unit vector.
% Mass Flow: (inlet marker, density, velocity magnitude, flow_direction_x,
% flow_direction_y, flow_direction_z, ... ) where flow_direction is
% a unit vector.
% Inc. Velocity: (inlet marker, temperature, velocity magnitude, flow_direction_x,
% flow_direction_y, flow_direction_z, ... ) where flow_direction is
% a unit vector.
% Inc. Pressure: (inlet marker, temperature, total pressure, flow_direction_x,
% flow_direction_y, flow_direction_z, ... ) where flow_direction is
% a unit vector.
%MARKER_INLET= ( INLET, 288.15, 101325.0, 1.0, 0.0, 0.0)
%
% Outlet boundary marker(s) (NONE = no marker)
% Compressible: ( outlet marker, back pressure (static thermodynamic), ... )
% Inc. Pressure: ( outlet marker, back pressure (static gauge in Pa), ... )
% Inc. Mass Flow: ( outlet marker, mass flow target (kg/s), ... )
%MARKER_OUTLET= ( OUTLET )
%
% ------------------------ WALL FUNCTION DEFINITION --------------------------%
%
% The von Karman constant, the constant below only affects the standard wall function model
WALLMODEL_KAPPA= 0.41
%
% The wall function model constant B
WALLMODEL_B= 5.5
%
% The y+ value below which the wall function is switched off and we resolve the wall
WALLMODEL_MINYPLUS= 5.0
%
% [Expert] Max Newton iterations used for the standard wall function
WALLMODEL_MAXITER= 200
%
% [Expert] relaxation factor for the Newton iterations of the standard wall function
WALLMODEL_RELFAC= 0.5
% ------------------------ SURFACES IDENTIFICATION ----------------------------%
%
% Marker(s) of the surface in the surface flow solution file
MARKER_PLOTTING = ( wing, wall, ground )
%
% Marker(s) of the surface where the non-dimensional coefficients are evaluated.
MARKER_MONITORING = ( wing )
%
% Viscous wall markers for which wall functions must be applied. (NONE = no marker)
% Format: ( marker name, wall function type -NO_WALL_FUNCTION, STANDARD_WALL_FUNCTION,
% ADAPTIVE_WALL_FUNCTION, SCALABLE_WALL_FUNCTION, EQUILIBRIUM_WALL_MODEL,
% NONEQUILIBRIUM_WALL_MODEL-, ... )
MARKER_WALL_FUNCTIONS= ( wing, NO_WALL_FUNCTION )
%
% Marker(s) of the surface where custom thermal BCs are defined.
MARKER_PYTHON_CUSTOM = ( NONE )
%
% Marker(s) of the surface that is going to be analyzed in detail (massflow, average pressure, distortion, etc)
MARKER_ANALYZE = ( wing )
%
% Method to compute the average value in MARKER_ANALYZE (AREA, MASSFLUX).
MARKER_ANALYZE_AVERAGE = AREA
% ------------- COMMON PARAMETERS DEFINING THE NUMERICAL METHOD ---------------%
%
% Numerical method for spatial gradients (GREEN_GAUSS, WEIGHTED_LEAST_SQUARES)
NUM_METHOD_GRAD= GREEN_GAUSS
% Numerical method for spatial gradients to be used for MUSCL reconstruction
% Options are (GREEN_GAUSS, WEIGHTED_LEAST_SQUARES, LEAST_SQUARES). Default value is
% NONE and the method specified in NUM_METHOD_GRAD is used.
NUM_METHOD_GRAD_RECON = NONE
%
% CFL number (initial value for the adaptive CFL number)
CFL_NUMBER= 1.0
%
% Adaptive CFL number (NO, YES)
CFL_ADAPT= NO
%
% Parameters of the adaptive CFL number (factor-down, factor-up, CFL min value,
% CFL max value, acceptable linear solver convergence)
% Local CFL increases by factor-up until max if the solution rate of change is not limited,
% and acceptable linear convergence is achieved. It is reduced if rate is limited, or if there
% is not enough linear convergence, or if the nonlinear residuals are stagnant and oscillatory.
% It is reset back to min when linear solvers diverge, or if nonlinear residuals increase too much.
CFL_ADAPT_PARAM= ( 0.1, 2.0, 10.0, 1e10, 0.001 )
%
% Maximum Delta Time in local time stepping simulations
MAX_DELTA_TIME= 1E6
%
% Runge-Kutta alpha coefficients
RK_ALPHA_COEFF= ( 0.66667, 0.66667, 1.000000 )
%
% Objective function in gradient evaluation (DRAG, LIFT, SIDEFORCE, MOMENT_X,
% MOMENT_Y, MOMENT_Z, EFFICIENCY, BUFFET,
% EQUIVALENT_AREA, NEARFIELD_PRESSURE,
% FORCE_X, FORCE_Y, FORCE_Z, THRUST,
% TORQUE, TOTAL_HEATFLUX, CUSTOM_OBJFUNC
% MAXIMUM_HEATFLUX, INVERSE_DESIGN_PRESSURE,
% INVERSE_DESIGN_HEATFLUX, SURFACE_TOTAL_PRESSURE,
% SURFACE_MASSFLOW, SURFACE_STATIC_PRESSURE, SURFACE_MACH)
% For a weighted sum of objectives: separate by commas, add OBJECTIVE_WEIGHT and MARKER_MONITORING in matching order.
OBJECTIVE_FUNCTION= DRAG
%
% List of weighting values when using more than one OBJECTIVE_FUNCTION. Separate by commas and match with MARKER_MONITORING.
OBJECTIVE_WEIGHT = 1.0
%
% Expression used when "OBJECTIVE_FUNCTION= CUSTOM_OBJFUNC", any history/screen output can be used together with common
% math functions (sqrt, cos, exp, etc.). This can be used for constraint aggregation (as below) or to compute something
% SU2 does not, see TestCases/user_defined_functions/.
CUSTOM_OBJFUNC= 'DRAG + 10 * pow(fmax(0.4-LIFT, 0), 2)'
% ----------- SLOPE LIMITER AND DISSIPATION SENSOR DEFINITION -----------------%
%
% Monotonic Upwind Scheme for Conservation Laws (TVD) in the flow equations.
% Required for 2nd order upwind schemes (NO, YES)
MUSCL_FLOW= YES
%
% Slope limiter (NONE, VENKATAKRISHNAN, VENKATAKRISHNAN_WANG,
% BARTH_JESPERSEN, VAN_ALBADA_EDGE)
SLOPE_LIMITER_FLOW= VENKATAKRISHNAN
%
% Monotonic Upwind Scheme for Conservation Laws (TVD) in the turbulence equations.
% Required for 2nd order upwind schemes (NO, YES)
MUSCL_TURB= NO
%
% Slope limiter (NONE, VENKATAKRISHNAN, VENKATAKRISHNAN_WANG,
% BARTH_JESPERSEN, VAN_ALBADA_EDGE)
SLOPE_LIMITER_TURB= VENKATAKRISHNAN
%
% Monotonic Upwind Scheme for Conservation Laws (TVD) in the adjoint flow equations.
% Required for 2nd order upwind schemes (NO, YES)
MUSCL_ADJFLOW= YES
%
% Slope limiter (NONE, VENKATAKRISHNAN, BARTH_JESPERSEN, VAN_ALBADA_EDGE,
% SHARP_EDGES, WALL_DISTANCE)
SLOPE_LIMITER_ADJFLOW= VENKATAKRISHNAN
%
% Monotonic Upwind Scheme for Conservation Laws (TVD) in the turbulence adjoint equations.
% Required for 2nd order upwind schemes (NO, YES)
MUSCL_ADJTURB= NO
%
% Slope limiter (NONE, VENKATAKRISHNAN, BARTH_JESPERSEN, VAN_ALBADA_EDGE)
SLOPE_LIMITER_ADJTURB= VENKATAKRISHNAN
%
% Coefficient for the Venkats limiter (upwind scheme). A larger values decrease
% the extent of limiting, values approaching zero cause
% lower-order approximation to the solution (0.05 by default)
VENKAT_LIMITER_COEFF= 0.05
%
% Reference coefficient for detecting sharp edges (3.0 by default).
REF_SHARP_EDGES = 3.0
%
% Coefficient for the adjoint sharp edges limiter (3.0 by default).
ADJ_SHARP_LIMITER_COEFF= 3.0
%
% Remove sharp edges from the sensitivity evaluation (NO, YES)
SENS_REMOVE_SHARP = NO
%
% Freeze the value of the limiter after a number of iterations
LIMITER_ITER= 999999
%
% 1st order artificial dissipation coefficients for
% the Lax–Friedrichs method ( 0.15 by default )
LAX_SENSOR_COEFF= 0.15
%
% 2nd and 4th order artificial dissipation coefficients for
% the JST method ( 0.5, 0.02 by default )
JST_SENSOR_COEFF= ( 0.5, 0.02 )
%
% 1st order artificial dissipation coefficients for
% the adjoint Lax–Friedrichs method ( 0.15 by default )
ADJ_LAX_SENSOR_COEFF= 0.15
%
% 2nd, and 4th order artificial dissipation coefficients for
% the adjoint JST method ( 0.5, 0.02 by default )
ADJ_JST_SENSOR_COEFF= ( 0.5, 0.02 )
% ------------------------ LINEAR SOLVER DEFINITION ---------------------------%
%
% Linear solver or smoother for implicit formulations:
% BCGSTAB, FGMRES, RESTARTED_FGMRES, CONJUGATE_GRADIENT (self-adjoint problems only), SMOOTHER.
LINEAR_SOLVER= FGMRES
%
% Same for discrete adjoint (smoothers not supported), replaces LINEAR_SOLVER in SU2_*_AD codes.
DISCADJ_LIN_SOLVER= FGMRES
%
% Preconditioner of the Krylov linear solver or type of smoother (ILU, LU_SGS, LINELET, JACOBI)
LINEAR_SOLVER_PREC= ILU
%
% Same for discrete adjoint (JACOBI or ILU), replaces LINEAR_SOLVER_PREC in SU2_*_AD codes.
DISCADJ_LIN_PREC= ILU
%
% Linear solver ILU preconditioner fill-in level (0 by default)
LINEAR_SOLVER_ILU_FILL_IN= 0
%
% Minimum error of the linear solver for implicit formulations
LINEAR_SOLVER_ERROR= 1E-6
%
% Max number of iterations of the linear solver for the implicit formulation
LINEAR_SOLVER_ITER= 5
%
% Restart frequency for RESTARTED_FGMRES
LINEAR_SOLVER_RESTART_FREQUENCY= 10
%
% Relaxation factor for smoother-type solvers (LINEAR_SOLVER= SMOOTHER)
LINEAR_SOLVER_SMOOTHER_RELAXATION= 1.0
%
% -------------------- FLOW NUMERICAL METHOD DEFINITION -----------------------%
%
% Convective numerical method (JST, JST_KE, JST_MAT, LAX-FRIEDRICH, CUSP, ROE, AUSM,
% AUSMPLUSUP, AUSMPLUSUP2, AUSMPWPLUS, HLLC, TURKEL_PREC,
% SW, MSW, FDS, SLAU, SLAU2, L2ROE, LMROE)
CONV_NUM_METHOD_FLOW= JST
%
% Roe Low Dissipation function for Hybrid RANS/LES simulations (FD, NTS, NTS_DUCROS)
ROE_LOW_DISSIPATION= FD
%
% Post-reconstruction correction for low Mach number flows (NO, YES)
LOW_MACH_CORR= NO
%
% Roe-Turkel preconditioning for low Mach number flows (NO, YES)
LOW_MACH_PREC= NO
%
% Use numerically computed Jacobians for AUSM+up(2) and SLAU(2)
% Slower per iteration but potentialy more stable and capable of higher CFL
USE_ACCURATE_FLUX_JACOBIANS= NO
%
% Use the vectorized version of the selected numerical method (available for JST family and Roe).
% SU2 should be compiled for an AVX or AVX512 architecture for best performance.
USE_VECTORIZATION= NO
%
% Entropy fix coefficient (0.0 implies no entropy fixing, 1.0 implies scalar
% artificial dissipation)
ENTROPY_FIX_COEFF= 0.0
%
% Higher values than 1 (3 to 4) make the global Jacobian of central schemes (compressible flow
% only) more diagonal dominant (but mathematically incorrect) so that higher CFL can be used.
CENTRAL_JACOBIAN_FIX_FACTOR= 4.0
%
% Time discretization (RUNGE-KUTTA_EXPLICIT, EULER_IMPLICIT, EULER_EXPLICIT)
TIME_DISCRE_FLOW= EULER_IMPLICIT
%
% Use a Newton-Krylov method on the flow equations, see TestCases/rans/oneram6/turb_ONERAM6_nk.cfg
% For multizone discrete adjoint it will use FGMRES on inner iterations with restart frequency
% equal to "QUASI_NEWTON_NUM_SAMPLES".
NEWTON_KRYLOV= NO
%
%
% -------------------- TURBULENT NUMERICAL METHOD DEFINITION ------------------%
%
% Convective numerical method (SCALAR_UPWIND)
CONV_NUM_METHOD_TURB= SCALAR_UPWIND
%
% Time discretization (EULER_IMPLICIT, EULER_EXPLICIT)
TIME_DISCRE_TURB= EULER_IMPLICIT
%
% Reduction factor of the CFL coefficient in the turbulence problem
CFL_REDUCTION_TURB= 1.0
%
% --------------------- HYBRID PARALLEL (MPI+OpenMP) OPTIONS ---------------------%
%
% An advanced performance parameter for FVM solvers, a large-ish value should be best
% when relatively few threads per MPI rank are in use (~4). However, maximum parallelism
% is obtained with EDGE_COLORING_GROUP_SIZE=1, consider using this value only if SU2
% warns about low coloring efficiency during preprocessing (performance is usually worse).
% Setting the option to 0 disables coloring and a different strategy is used instead,
% that strategy is automatically used when the coloring efficiency is less than 0.875.
% The optimum value/strategy is case-dependent.
EDGE_COLORING_GROUP_SIZE= 512
%
% Independent "threads per MPI rank" setting for LU-SGS and ILU preconditioners.
% For problems where time is spend mostly in the solution of linear systems (e.g. elasticity,
% very high CFL central schemes), AND, if the memory bandwidth of the machine is saturated
% (4 or more cores per memory channel) better performance (via a reduction in linear iterations)
% may be possible by using a smaller value than that defined by the system or in the call to
% SU2_CFD (via the -t/--threads option).
% The default (0) means "same number of threads as for all else".
LINEAR_SOLVER_PREC_THREADS= 0
%
% ----------------------- PARTITIONING OPTIONS (ParMETIS) ------------------------ %
%
% Load balancing tolerance, lower values will make ParMETIS work harder to evenly
% distribute the work-estimate metric across all MPI ranks, at the expense of more
% edge cuts (i.e. increased communication cost).
PARMETIS_TOLERANCE= 0.02
%
% The work-estimate metric is a weighted function of the work-per-edge (e.g. spatial
% discretization, linear system solution) and of the work-per-point (e.g. source terms,
% temporal discretization) the former usually accounts for >90% of the total.
% These weights are INTEGERS (for compatibility with ParMETIS) thus not [0, 1].
% To balance memory usage (instead of computation) the point weight needs to be
% increased (especially for explicit time integration methods).
PARMETIS_EDGE_WEIGHT= 1
PARMETIS_POINT_WEIGHT= 0
%
%
% ------------------------- SCREEN/HISTORY VOLUME OUTPUT --------------------------%
%
% Screen output fields (use 'SU2_CFD -d <config_file>' to view list of available fields)
SCREEN_OUTPUT= (INNER_ITER, PRESSURE, RMS_VELOCITY, SIDEFORCE, DRAG, LIFT)
%
% History output groups (use 'SU2_CFD -d <config_file>' to view list of available fields)
HISTORY_OUTPUT= (ITER, RMS_PRESSURE, RMS_VELOCITY, SIDEFORCE, DRAG, LIFT)
%
% Volume output fields/groups (use 'SU2_CFD -d <config_file>' to view list of available fields)
VOLUME_OUTPUT= (COORDINATES, SOLUTION, PRIMITIVE)
%
% Writing frequency for screen output
SCREEN_WRT_FREQ_INNER= 1
%
SCREEN_WRT_FREQ_OUTER= 1
%
SCREEN_WRT_FREQ_TIME= 1
%
% Writing frequency for history output
HISTORY_WRT_FREQ_INNER= 1
%
HISTORY_WRT_FREQ_OUTER= 1
%
HISTORY_WRT_FREQ_TIME= 1
%
% list of writing frequencies corresponding to the list in OUTPUT_FILES
OUTPUT_WRT_FREQ= 250, 250, 300
%
% Output the performance summary to the console at the end of SU2_CFD
WRT_PERFORMANCE= NO
%
% Overwrite or append iteration number to the restart files when saving
WRT_RESTART_OVERWRITE= YES
%
% Overwrite or append iteration number to the surface files when saving
WRT_SURFACE_OVERWRITE= YES
%
% Overwrite or append iteration number to the volume files when saving
WRT_VOLUME_OVERWRITE= YES
%
% ------------------------- INPUT/OUTPUT FILE INFORMATION --------------------------%
%
% Mesh input file
MESH_FILENAME= mesh_h17.su2
%
% Mesh input file format (SU2, CGNS)
MESH_FORMAT= SU2
%
% Mesh output file
MESH_OUT_FILENAME= mesh_h17.su2
%
% Restart flow input file
SOLUTION_FILENAME= solution_flow.dat
%
% Restart adjoint input file
SOLUTION_ADJ_FILENAME= solution_adj.dat
%
% Output tabular file format (TECPLOT, CSV)
TABULAR_FORMAT= CSV
%
% Files to output
% Possible formats : (TECPLOT_ASCII, TECPLOT, SURFACE_TECPLOT_ASCII,
% SURFACE_TECPLOT, CSV, SURFACE_CSV, PARAVIEW_ASCII, PARAVIEW_LEGACY, SURFACE_PARAVIEW_ASCII,
% SURFACE_PARAVIEW_LEGACY, PARAVIEW, SURFACE_PARAVIEW, RESTART_ASCII, RESTART, CGNS, SURFACE_CGNS, STL_ASCII, STL_BINARY)
% default : (RESTART, PARAVIEW, SURFACE_PARAVIEW)
OUTPUT_FILES= (RESTART, PARAVIEW, SURFACE_PARAVIEW)
%
% Output file convergence history (w/o extension)
CONV_FILENAME= history
%
% Output file with the forces breakdown
BREAKDOWN_FILENAME= forces_breakdown.dat
%
% Output file restart flow
RESTART_FILENAME= restart_flow.dat
%
% Output file flow (w/o extension) variables
VOLUME_FILENAME= flow
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% %
% SU2 configuration file %
% Case description: Tyrrell 026 Front Wing in Wind Tunnel____________________ %
% Author: Matheus Ribeiro Vidal______________________________________________ %
% Institution: Universidade de Brasilia______________________________________ %
% Date: 28/01/2023 %
% File Version 7.3.1 "Blackbird" %
% %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% ------------- DIRECT, ADJOINT, AND LINEARIZED PROBLEM DEFINITION ------------%
%
% Solver type (EULER, NAVIER_STOKES, RANS,
% INC_EULER, INC_NAVIER_STOKES, INC_RANS,
% NEMO_EULER, NEMO_NAVIER_STOKES,
% FEM_EULER, FEM_NAVIER_STOKES, FEM_RANS, FEM_LES,
% HEAT_EQUATION_FVM, ELASTICITY)
SOLVER= INC_RANS
%
% Specify turbulence model (NONE, SA, SA_NEG, SST, SA_E, SA_COMP, SA_E_COMP, SST_SUST)
KIND_TURB_MODEL= SST
%
% Mathematical problem (DIRECT, CONTINUOUS_ADJOINT, DISCRETE_ADJOINT)
% Defaults to DISCRETE_ADJOINT for the SU2_*_AD codes, and to DIRECT otherwise.
MATH_PROBLEM= DIRECT
%
% System of measurements (SI, US)
% International system of units (SI): ( meters, kilograms, Kelvins,
% Newtons = kg m/s^2, Pascals = N/m^2,
% Density = kg/m^3, Speed = m/s,
% Equiv. Area = m^2 )
SYSTEM_MEASUREMENTS= SI
%
%
% ------------------------------- SOLVER CONTROL ------------------------------%
%
% Number of iterations for single-zone problems
ITER= 1
%
% Maximum number of inner iterations
INNER_ITER= 15000
%
% Maximum number of outer iterations (only for multizone problems)
OUTER_ITER= 1
%
% Maximum number of time iterations
TIME_ITER= 1
%
% Convergence field
CONV_FIELD= PRESSURE
%
% Min value of the residual (log10 of the residual)
CONV_RESIDUAL_MINVAL= -8
%
% Start convergence criteria at iteration number
CONV_STARTITER= 10
%
% Number of elements to apply the criteria
CONV_CAUCHY_ELEMS= 100
%
% Epsilon to control the series convergence
CONV_CAUCHY_EPS= 1E-10
%
% Iteration number to begin unsteady restarts
RESTART_ITER= 0
%
%% Time convergence monitoring
WINDOW_CAUCHY_CRIT = YES
%
% List of time convergence fields
CONV_WINDOW_FIELD = (TAVG_DRAG, TAVG_LIFT)
%
% Time Convergence Monitoring starts at Iteration WINDOW_START_ITER + CONV_WINDOW_STARTITER
CONV_WINDOW_STARTITER = 0
%
% Epsilon to control the series convergence
CONV_WINDOW_CAUCHY_EPS = 1E-3
%
% Number of elements to apply the criteria
CONV_WINDOW_CAUCHY_ELEMS = 10
%
% ------------------------- TIME-DEPENDENT SIMULATION -------------------------------%
%
% Time domain simulation
TIME_DOMAIN= NO
%
% Unsteady simulation (NO, TIME_STEPPING, DUAL_TIME_STEPPING-1ST_ORDER,
% DUAL_TIME_STEPPING-2ND_ORDER, HARMONIC_BALANCE)
TIME_MARCHING= NO
%
% Time Step for dual time stepping simulations (s) -- Only used when UNST_CFL_NUMBER = 0.0
% For the DG-FEM solver it is used as a synchronization time when UNST_CFL_NUMBER != 0.0
TIME_STEP= 0.00001
%
% Total Physical Time for dual time stepping simulations (s)
MAX_TIME= 2.0
%
% Unsteady Courant-Friedrichs-Lewy number of the finest grid
UNST_CFL_NUMBER= 1.0
%
%% Windowed output time averaging
% Time iteration to start the windowed time average in a direct run
WINDOW_START_ITER = 500
%
% Window used for reverse sweep and direct run. Options (SQUARE, HANN, HANN_SQUARE, BUMP) Square is default.
WINDOW_FUNCTION = SQUARE
%
% ------------------------------- DES Parameters ------------------------------%
%
% Specify Hybrid RANS/LES model (SA_DES, SA_DDES, SA_ZDES, SA_EDDES)
HYBRID_RANSLES= SA_DDES
%
% DES Constant (0.65)
DES_CONST= 0.65
%
% ---------------- INCOMPRESSIBLE FLOW CONDITION DEFINITION -------------------%
%
% Density model within the incompressible flow solver.
% Options are CONSTANT (default), BOUSSINESQ, or VARIABLE. If VARIABLE,
% an appropriate fluid model must be selected.
INC_DENSITY_MODEL= CONSTANT
%
% Solve the energy equation in the incompressible flow solver
INC_ENERGY_EQUATION = NO
%
% Initial density for incompressible flows
% (1.2886 kg/m^3 by default (air), 998.2 Kg/m^3 (water))
INC_DENSITY_INIT= 1.2886
%
% Initial velocity for incompressible flows (1.0,0,0 m/s by default)
INC_VELOCITY_INIT= ( 30.0, 0.0, 0.0 )
%
% Initial temperature for incompressible flows that include the
% energy equation (288.15 K by default). Value is ignored if
% INC_ENERGY_EQUATION is false.
INC_TEMPERATURE_INIT= 288.15
%
% Non-dimensionalization scheme for incompressible flows. Options are
% INITIAL_VALUES (default), REFERENCE_VALUES, or DIMENSIONAL.
% INC_*_REF values are ignored unless REFERENCE_VALUES is chosen.
INC_NONDIM= INITIAL_VALUES
%
% Reference density for incompressible flows (1.0 kg/m^3 by default)
INC_DENSITY_REF= 1.0
%
% Reference velocity for incompressible flows (1.0 m/s by default)
INC_VELOCITY_REF= 1.0
%
% Reference temperature for incompressible flows that include the
% energy equation (1.0 K by default)
INC_TEMPERATURE_REF = 1.0
%
% List of inlet types for incompressible flows. List length must
% match number of inlet markers. Options: VELOCITY_INLET, PRESSURE_INLET.
INC_INLET_TYPE= VELOCITY_INLET
%
% Damping coefficient for iterative updates at pressure inlets. (0.1 by default)
INC_INLET_DAMPING= 0.1
%
% List of outlet types for incompressible flows. List length must
% match number of outlet markers. Options: PRESSURE_OUTLET, MASS_FLOW_OUTLET
INC_OUTLET_TYPE= PRESSURE_OUTLET
%
% Damping coefficient for iterative updates at mass flow outlets. (0.1 by default)
INC_OUTLET_DAMPING= 0.1
%
% Epsilon^2 multipier in Beta calculation for incompressible preconditioner.
BETA_FACTOR= 4.1
%
% ---------------------- REFERENCE VALUE DEFINITION ---------------------------%
%
% Reference origin for moment computation (m or in) % Atualmente em um quarto de Asa
REF_ORIGIN_MOMENT_X = 0.00
REF_ORIGIN_MOMENT_Y = 0.00
REF_ORIGIN_MOMENT_Z = 0.00
%
% Reference length for moment non-dimensional coefficients (m or in)
REF_LENGTH= 0.380
%
% Reference area for non-dimensional force coefficients (0 implies automatic
% calculation) (m^2 or in^2)
REF_AREA= 0.405
%
% Aircraft semi-span (0 implies automatic calculation) (m or in)
SEMI_SPAN= 0.0
%
% --------------------------- VISCOSITY MODEL ---------------------------------%
%
% Viscosity model (SUTHERLAND, CONSTANT_VISCOSITY, POLYNOMIAL_VISCOSITY).
VISCOSITY_MODEL= CONSTANT_VISCOSITY
% Molecular Viscosity that would be constant (1.716E-5 by default)
MU_CONSTANT= 1.716E-5
%
% Sutherland Viscosity Ref (1.716E-5 default value for AIR SI)
MU_REF= 1.716E-5
%
% Sutherland Temperature Ref (273.15 K default value for AIR SI)
MU_T_REF= 273.15
%
% Sutherland constant (110.4 default value for AIR SI)
SUTHERLAND_CONSTANT= 110.4
%
% Temperature polynomial coefficients (up to quartic) for viscosity.
% Format -> Mu(T) : b0 + b1*T + b2*T^2 + b3*T^3 + b4*T^4
MU_POLYCOEFFS= (0.0, 0.0, 0.0, 0.0, 0.0)
%
% ----------------------- DYNAMIC MESH DEFINITION -----------------------------%
%
% Type of dynamic surface movement (NONE, DEFORMING, MOVING_WALL,
% AEROELASTIC, AEROELASTIC_RIGID_MOTION EXTERNAL, EXTERNAL_ROTATION)
SURFACE_MOVEMENT= NONE
%
% Moving wall boundary marker(s) (NONE = no marker, ignored for RIGID_MOTION)
% MARKER_MOVING= ( NONE )
%
% Coordinates of the motion origin
% SURFACE_MOTION_ORIGIN= -4 0.0 0.0
%
% Translational velocity (m/s or ft/s) in the x, y, & z directions
% SURFACE_TRANSLATION_RATE = 30.0 0.0 0.0
%
%
% Move Motion Origin for marker moving (1 or 0)
% MOVE_MOTION_ORIGIN = 0
%
% -------------------- BOUNDARY CONDITION DEFINITION --------------------------%
%
% Euler wall boundary marker(s) (NONE = no marker)
% Implementation identical to MARKER_SYM.
MARKER_EULER= ( NONE )
%
% Navier-Stokes (no-slip), constant heat flux wall marker(s) (NONE = no marker)
% Format: ( marker name, constant heat flux (J/m^2), ... )
MARKER_HEATFLUX= ( wing, 0)
%
% Far-field boundary marker(s) (NONE = no marker)
MARKER_FAR= ( inlet, outlet )
%
% Inlet boundary type (TOTAL_CONDITIONS, MASS_FLOW)
%
%INLET_TYPE= TOTAL_CONDITIONS
%
% Inlet boundary marker(s) with the following formats (NONE = no marker)
% Total Conditions: (inlet marker, total temp, total pressure, flow_direction_x,
% flow_direction_y, flow_direction_z, ... ) where flow_direction is
% a unit vector.
% Mass Flow: (inlet marker, density, velocity magnitude, flow_direction_x,
% flow_direction_y, flow_direction_z, ... ) where flow_direction is
% a unit vector.
% Inc. Velocity: (inlet marker, temperature, velocity magnitude, flow_direction_x,
% flow_direction_y, flow_direction_z, ... ) where flow_direction is
% a unit vector.
% Inc. Pressure: (inlet marker, temperature, total pressure, flow_direction_x,
% flow_direction_y, flow_direction_z, ... ) where flow_direction is
% a unit vector.
%MARKER_INLET= ( INLET, 288.15, 101325.0, 1.0, 0.0, 0.0)
%
% Outlet boundary marker(s) (NONE = no marker)
% Compressible: ( outlet marker, back pressure (static thermodynamic), ... )
% Inc. Pressure: ( outlet marker, back pressure (static gauge in Pa), ... )
% Inc. Mass Flow: ( outlet marker, mass flow target (kg/s), ... )
%MARKER_OUTLET= ( OUTLET )
%
% ------------------------ WALL FUNCTION DEFINITION --------------------------%
%
% The von Karman constant, the constant below only affects the standard wall function model
WALLMODEL_KAPPA= 0.41
%
% The wall function model constant B
WALLMODEL_B= 5.5
%
% The y+ value below which the wall function is switched off and we resolve the wall
WALLMODEL_MINYPLUS= 5.0
%
% [Expert] Max Newton iterations used for the standard wall function
WALLMODEL_MAXITER= 200
%
% [Expert] relaxation factor for the Newton iterations of the standard wall function
WALLMODEL_RELFAC= 0.5
% ------------------------ SURFACES IDENTIFICATION ----------------------------%
%
% Marker(s) of the surface in the surface flow solution file
MARKER_PLOTTING = ( wing )
%
% Marker(s) of the surface where the non-dimensional coefficients are evaluated.
MARKER_MONITORING = ( wing )
%
% Viscous wall markers for which wall functions must be applied. (NONE = no marker)
% Format: ( marker name, wall function type -NO_WALL_FUNCTION, STANDARD_WALL_FUNCTION,
% ADAPTIVE_WALL_FUNCTION, SCALABLE_WALL_FUNCTION, EQUILIBRIUM_WALL_MODEL,
% NONEQUILIBRIUM_WALL_MODEL-, ... )
MARKER_WALL_FUNCTIONS= ( wing, NO_WALL_FUNCTION )
%
% Marker(s) of the surface where custom thermal BCs are defined.
MARKER_PYTHON_CUSTOM = ( NONE )
%
% Marker(s) of the surface that is going to be analyzed in detail (massflow, average pressure, distortion, etc)
MARKER_ANALYZE = ( wing )
%
% Method to compute the average value in MARKER_ANALYZE (AREA, MASSFLUX).
MARKER_ANALYZE_AVERAGE = AREA
% ------------- COMMON PARAMETERS DEFINING THE NUMERICAL METHOD ---------------%
%
% Numerical method for spatial gradients (GREEN_GAUSS, WEIGHTED_LEAST_SQUARES)
NUM_METHOD_GRAD= GREEN_GAUSS
% Numerical method for spatial gradients to be used for MUSCL reconstruction
% Options are (GREEN_GAUSS, WEIGHTED_LEAST_SQUARES, LEAST_SQUARES). Default value is
% NONE and the method specified in NUM_METHOD_GRAD is used.
NUM_METHOD_GRAD_RECON = NONE
%
% CFL number (initial value for the adaptive CFL number)
CFL_NUMBER= 1.0
%
% Adaptive CFL number (NO, YES)
CFL_ADAPT= NO
%
% Parameters of the adaptive CFL number (factor-down, factor-up, CFL min value,
% CFL max value, acceptable linear solver convergence)
% Local CFL increases by factor-up until max if the solution rate of change is not limited,
% and acceptable linear convergence is achieved. It is reduced if rate is limited, or if there
% is not enough linear convergence, or if the nonlinear residuals are stagnant and oscillatory.
% It is reset back to min when linear solvers diverge, or if nonlinear residuals increase too much.
CFL_ADAPT_PARAM= ( 0.1, 2.0, 10.0, 1e10, 0.001 )
%
% Maximum Delta Time in local time stepping simulations
MAX_DELTA_TIME= 1E6
%
% Runge-Kutta alpha coefficients
RK_ALPHA_COEFF= ( 0.66667, 0.66667, 1.000000 )
%
% Objective function in gradient evaluation (DRAG, LIFT, SIDEFORCE, MOMENT_X,
% MOMENT_Y, MOMENT_Z, EFFICIENCY, BUFFET,
% EQUIVALENT_AREA, NEARFIELD_PRESSURE,
% FORCE_X, FORCE_Y, FORCE_Z, THRUST,
% TORQUE, TOTAL_HEATFLUX, CUSTOM_OBJFUNC
% MAXIMUM_HEATFLUX, INVERSE_DESIGN_PRESSURE,
% INVERSE_DESIGN_HEATFLUX, SURFACE_TOTAL_PRESSURE,
% SURFACE_MASSFLOW, SURFACE_STATIC_PRESSURE, SURFACE_MACH)
% For a weighted sum of objectives: separate by commas, add OBJECTIVE_WEIGHT and MARKER_MONITORING in matching order.
OBJECTIVE_FUNCTION= DRAG
%
% List of weighting values when using more than one OBJECTIVE_FUNCTION. Separate by commas and match with MARKER_MONITORING.
OBJECTIVE_WEIGHT = 1.0
%
% Expression used when "OBJECTIVE_FUNCTION= CUSTOM_OBJFUNC", any history/screen output can be used together with common
% math functions (sqrt, cos, exp, etc.). This can be used for constraint aggregation (as below) or to compute something
% SU2 does not, see TestCases/user_defined_functions/.
CUSTOM_OBJFUNC= 'DRAG + 10 * pow(fmax(0.4-LIFT, 0), 2)'
% ----------- SLOPE LIMITER AND DISSIPATION SENSOR DEFINITION -----------------%
%
% Monotonic Upwind Scheme for Conservation Laws (TVD) in the flow equations.
% Required for 2nd order upwind schemes (NO, YES)
MUSCL_FLOW= YES
%
% Slope limiter (NONE, VENKATAKRISHNAN, VENKATAKRISHNAN_WANG,
% BARTH_JESPERSEN, VAN_ALBADA_EDGE)
SLOPE_LIMITER_FLOW= VENKATAKRISHNAN
%
% Monotonic Upwind Scheme for Conservation Laws (TVD) in the turbulence equations.
% Required for 2nd order upwind schemes (NO, YES)
MUSCL_TURB= NO
%
% Slope limiter (NONE, VENKATAKRISHNAN, VENKATAKRISHNAN_WANG,
% BARTH_JESPERSEN, VAN_ALBADA_EDGE)
SLOPE_LIMITER_TURB= VENKATAKRISHNAN
%
% Monotonic Upwind Scheme for Conservation Laws (TVD) in the adjoint flow equations.
% Required for 2nd order upwind schemes (NO, YES)
MUSCL_ADJFLOW= YES
%
% Slope limiter (NONE, VENKATAKRISHNAN, BARTH_JESPERSEN, VAN_ALBADA_EDGE,
% SHARP_EDGES, WALL_DISTANCE)
SLOPE_LIMITER_ADJFLOW= VENKATAKRISHNAN
%
% Monotonic Upwind Scheme for Conservation Laws (TVD) in the turbulence adjoint equations.
% Required for 2nd order upwind schemes (NO, YES)
MUSCL_ADJTURB= NO
%
% Slope limiter (NONE, VENKATAKRISHNAN, BARTH_JESPERSEN, VAN_ALBADA_EDGE)
SLOPE_LIMITER_ADJTURB= VENKATAKRISHNAN
%
% Coefficient for the Venkats limiter (upwind scheme). A larger values decrease
% the extent of limiting, values approaching zero cause
% lower-order approximation to the solution (0.05 by default)
VENKAT_LIMITER_COEFF= 0.05
%
% Reference coefficient for detecting sharp edges (3.0 by default).
REF_SHARP_EDGES = 3.0
%
% Coefficient for the adjoint sharp edges limiter (3.0 by default).
ADJ_SHARP_LIMITER_COEFF= 3.0
%
% Remove sharp edges from the sensitivity evaluation (NO, YES)
SENS_REMOVE_SHARP = NO
%
% Freeze the value of the limiter after a number of iterations
LIMITER_ITER= 999999
%
% 1st order artificial dissipation coefficients for
% the Lax–Friedrichs method ( 0.15 by default )
LAX_SENSOR_COEFF= 0.15
%
% 2nd and 4th order artificial dissipation coefficients for
% the JST method ( 0.5, 0.02 by default )
JST_SENSOR_COEFF= ( 0.5, 0.02 )
%
% 1st order artificial dissipation coefficients for
% the adjoint Lax–Friedrichs method ( 0.15 by default )
ADJ_LAX_SENSOR_COEFF= 0.15
%
% 2nd, and 4th order artificial dissipation coefficients for
% the adjoint JST method ( 0.5, 0.02 by default )
ADJ_JST_SENSOR_COEFF= ( 0.5, 0.02 )
% ------------------------ LINEAR SOLVER DEFINITION ---------------------------%
%
% Linear solver or smoother for implicit formulations:
% BCGSTAB, FGMRES, RESTARTED_FGMRES, CONJUGATE_GRADIENT (self-adjoint problems only), SMOOTHER.
LINEAR_SOLVER= FGMRES
%
% Same for discrete adjoint (smoothers not supported), replaces LINEAR_SOLVER in SU2_*_AD codes.
DISCADJ_LIN_SOLVER= FGMRES
%
% Preconditioner of the Krylov linear solver or type of smoother (ILU, LU_SGS, LINELET, JACOBI)
LINEAR_SOLVER_PREC= ILU
%
% Same for discrete adjoint (JACOBI or ILU), replaces LINEAR_SOLVER_PREC in SU2_*_AD codes.
DISCADJ_LIN_PREC= ILU
%
% Linear solver ILU preconditioner fill-in level (0 by default)
LINEAR_SOLVER_ILU_FILL_IN= 0
%
% Minimum error of the linear solver for implicit formulations
LINEAR_SOLVER_ERROR= 1E-6
%
% Max number of iterations of the linear solver for the implicit formulation
LINEAR_SOLVER_ITER= 5
%
% Restart frequency for RESTARTED_FGMRES
LINEAR_SOLVER_RESTART_FREQUENCY= 10
%
% Relaxation factor for smoother-type solvers (LINEAR_SOLVER= SMOOTHER)
LINEAR_SOLVER_SMOOTHER_RELAXATION= 1.0
%
% -------------------- FLOW NUMERICAL METHOD DEFINITION -----------------------%
%
% Convective numerical method (JST, JST_KE, JST_MAT, LAX-FRIEDRICH, CUSP, ROE, AUSM,
% AUSMPLUSUP, AUSMPLUSUP2, AUSMPWPLUS, HLLC, TURKEL_PREC,
% SW, MSW, FDS, SLAU, SLAU2, L2ROE, LMROE)
CONV_NUM_METHOD_FLOW= JST
%
% Roe Low Dissipation function for Hybrid RANS/LES simulations (FD, NTS, NTS_DUCROS)
ROE_LOW_DISSIPATION= FD
%
% Post-reconstruction correction for low Mach number flows (NO, YES)
LOW_MACH_CORR= NO
%
% Roe-Turkel preconditioning for low Mach number flows (NO, YES)
LOW_MACH_PREC= NO
%
% Use numerically computed Jacobians for AUSM+up(2) and SLAU(2)
% Slower per iteration but potentialy more stable and capable of higher CFL
USE_ACCURATE_FLUX_JACOBIANS= NO
%
% Use the vectorized version of the selected numerical method (available for JST family and Roe).
% SU2 should be compiled for an AVX or AVX512 architecture for best performance.
USE_VECTORIZATION= NO
%
% Entropy fix coefficient (0.0 implies no entropy fixing, 1.0 implies scalar
% artificial dissipation)
ENTROPY_FIX_COEFF= 0.0
%
% Higher values than 1 (3 to 4) make the global Jacobian of central schemes (compressible flow
% only) more diagonal dominant (but mathematically incorrect) so that higher CFL can be used.
CENTRAL_JACOBIAN_FIX_FACTOR= 4.0
%
% Time discretization (RUNGE-KUTTA_EXPLICIT, EULER_IMPLICIT, EULER_EXPLICIT)
TIME_DISCRE_FLOW= EULER_IMPLICIT
%
% Use a Newton-Krylov method on the flow equations, see TestCases/rans/oneram6/turb_ONERAM6_nk.cfg
% For multizone discrete adjoint it will use FGMRES on inner iterations with restart frequency
% equal to "QUASI_NEWTON_NUM_SAMPLES".
NEWTON_KRYLOV= NO
%
%
% -------------------- TURBULENT NUMERICAL METHOD DEFINITION ------------------%
%
% Convective numerical method (SCALAR_UPWIND)
CONV_NUM_METHOD_TURB= SCALAR_UPWIND
%
% Time discretization (EULER_IMPLICIT, EULER_EXPLICIT)
TIME_DISCRE_TURB= EULER_IMPLICIT
%
% Reduction factor of the CFL coefficient in the turbulence problem
CFL_REDUCTION_TURB= 1.0
%
% --------------------- HYBRID PARALLEL (MPI+OpenMP) OPTIONS ---------------------%
%
% An advanced performance parameter for FVM solvers, a large-ish value should be best
% when relatively few threads per MPI rank are in use (~4). However, maximum parallelism
% is obtained with EDGE_COLORING_GROUP_SIZE=1, consider using this value only if SU2
% warns about low coloring efficiency during preprocessing (performance is usually worse).
% Setting the option to 0 disables coloring and a different strategy is used instead,
% that strategy is automatically used when the coloring efficiency is less than 0.875.
% The optimum value/strategy is case-dependent.
EDGE_COLORING_GROUP_SIZE= 512
%
% Independent "threads per MPI rank" setting for LU-SGS and ILU preconditioners.
% For problems where time is spend mostly in the solution of linear systems (e.g. elasticity,
% very high CFL central schemes), AND, if the memory bandwidth of the machine is saturated
% (4 or more cores per memory channel) better performance (via a reduction in linear iterations)
% may be possible by using a smaller value than that defined by the system or in the call to
% SU2_CFD (via the -t/--threads option).
% The default (0) means "same number of threads as for all else".
LINEAR_SOLVER_PREC_THREADS= 0
%
% ----------------------- PARTITIONING OPTIONS (ParMETIS) ------------------------ %
%
% Load balancing tolerance, lower values will make ParMETIS work harder to evenly
% distribute the work-estimate metric across all MPI ranks, at the expense of more
% edge cuts (i.e. increased communication cost).
PARMETIS_TOLERANCE= 0.02
%
% The work-estimate metric is a weighted function of the work-per-edge (e.g. spatial
% discretization, linear system solution) and of the work-per-point (e.g. source terms,
% temporal discretization) the former usually accounts for >90% of the total.
% These weights are INTEGERS (for compatibility with ParMETIS) thus not [0, 1].
% To balance memory usage (instead of computation) the point weight needs to be
% increased (especially for explicit time integration methods).
PARMETIS_EDGE_WEIGHT= 1
PARMETIS_POINT_WEIGHT= 0
%
%
% ------------------------- SCREEN/HISTORY VOLUME OUTPUT --------------------------%
%
% Screen output fields (use 'SU2_CFD -d <config_file>' to view list of available fields)
SCREEN_OUTPUT= (INNER_ITER, PRESSURE, RMS_VELOCITY, SIDEFORCE, DRAG, LIFT)
%
% History output groups (use 'SU2_CFD -d <config_file>' to view list of available fields)
HISTORY_OUTPUT= (ITER, RMS_PRESSURE, RMS_VELOCITY, SIDEFORCE, DRAG, LIFT)
%
% Volume output fields/groups (use 'SU2_CFD -d <config_file>' to view list of available fields)
VOLUME_OUTPUT= (COORDINATES, SOLUTION, PRIMITIVE)
%
% Writing frequency for screen output
SCREEN_WRT_FREQ_INNER= 1
%
SCREEN_WRT_FREQ_OUTER= 1
%
SCREEN_WRT_FREQ_TIME= 1
%
% Writing frequency for history output
HISTORY_WRT_FREQ_INNER= 1
%
HISTORY_WRT_FREQ_OUTER= 1
%
HISTORY_WRT_FREQ_TIME= 1
%
% list of writing frequencies corresponding to the list in OUTPUT_FILES
OUTPUT_WRT_FREQ= 250, 250, 300
%
% Output the performance summary to the console at the end of SU2_CFD
WRT_PERFORMANCE= NO
%
% Overwrite or append iteration number to the restart files when saving
WRT_RESTART_OVERWRITE= YES
%
% Overwrite or append iteration number to the surface files when saving
WRT_SURFACE_OVERWRITE= YES
%
% Overwrite or append iteration number to the volume files when saving
WRT_VOLUME_OVERWRITE= YES
%
% ------------------------- INPUT/OUTPUT FILE INFORMATION --------------------------%
%
% Mesh input file
MESH_FILENAME= hinf.su2
%
% Mesh input file format (SU2, CGNS)
MESH_FORMAT= SU2
%
% Mesh output file
MESH_OUT_FILENAME= hinf.su2
%
% Restart flow input file
SOLUTION_FILENAME= solution_flow.dat
%
% Restart adjoint input file
SOLUTION_ADJ_FILENAME= solution_adj.dat
%
% Output tabular file format (TECPLOT, CSV)
TABULAR_FORMAT= CSV
%
% Files to output
% Possible formats : (TECPLOT_ASCII, TECPLOT, SURFACE_TECPLOT_ASCII,
% SURFACE_TECPLOT, CSV, SURFACE_CSV, PARAVIEW_ASCII, PARAVIEW_LEGACY, SURFACE_PARAVIEW_ASCII,
% SURFACE_PARAVIEW_LEGACY, PARAVIEW, SURFACE_PARAVIEW, RESTART_ASCII, RESTART, CGNS, SURFACE_CGNS, STL_ASCII, STL_BINARY)
% default : (RESTART, PARAVIEW, SURFACE_PARAVIEW)
OUTPUT_FILES= (RESTART, PARAVIEW, SURFACE_PARAVIEW)
%
% Output file convergence history (w/o extension)
CONV_FILENAME= history
%
% Output file with the forces breakdown
BREAKDOWN_FILENAME= forces_breakdown.dat
%
% Output file restart flow
RESTART_FILENAME= restart_flow.dat
%
% Output file flow (w/o extension) variables
VOLUME_FILENAME= flow
%
Python QOL scripts
import os
import csv
import numpy as np
import matplotlib.pyplot as plt
# Important folder PATHs
print('Aonde esse script ta rodando?')
print('1. PC do Matheus')
print('2. Cluster Amadea')
print("")
machine = input()
print("")
print("###################################################################")
if machine == '1':
base_folder = r'C:\Users\mathe\Documents\Meus Arquivos\UnB\Projeto de Pesquisa\Cluster Mirror\pg2'
history_plotter_fig_plain_path = r'C:\Users\mathe\Documents\Meus Arquivos\UnB\Projeto de Pesquisa\Cluster Mirror\pg2\pg_files\results\History Plotter Figs\Plain'
history_plotter_fig_full_path = r'C:\Users\mathe\Documents\Meus Arquivos\UnB\Projeto de Pesquisa\Cluster Mirror\pg2\pg_files\results\History Plotter Figs\Full'
simulating_folder_name = r'Simulating'
results_file_path = r'C:\Users\mathe\Documents\Meus Arquivos\UnB\Projeto de Pesquisa\Cluster Mirror\pg2\pg_files\results'
else:
base_folder = r'/home/matheus/pg2'
history_plotter_fig_plain_path = r'/home/matheus/pg2/pg_files/results/History Plotter Figs/Plain'
history_plotter_fig_full_path = r'/home/matheus/pg2/pg_files/results/History Plotter Figs/Full'
simulating_folder_name = r'Simulating'
results_file_path = r'/home/matheus/pg2/pg_files/results'
folders_to_check = [17, 20, 22, 25, 27, 30, 32, 35, 37, 40, 45, 50, 60, 70, 80, 85, 90, 95, 100, 110, 120, 130, 150, 225, 'inf']
# Separate integers and strings
integers = []
strings = []
for item in folders_to_check:
if isinstance(item, int):
integers.append(item)
else:
strings.append(item)
# Sort the integer list in ascending order
sorted_integers = sorted(integers)
# Sort the string list
sorted_strings = sorted(strings)
# Concatenate the sorted integer list with the sorted string list
sorted_folders = sorted_strings + sorted_integers
print('')
for case_number in sorted_folders:
folder_name = f'h{case_number}'
mesh_filename = f'mesh_h{case_number}.su2'
output_filename = 'output.dat'
folder_path = os.path.join(base_folder, folder_name)
output_filepath = os.path.join(folder_path, output_filename)
history_file = os.path.join(folder_path, 'history.csv')
mesh_file = os.path.join(folder_path,mesh_filename)
print(folder_name)
print("")
print(f"Checking folder: {folder_path}")
if os.path.exists(history_file):
target_string = "grid points before partitioning"
with open(output_filepath, "r") as file:
lines = file.readlines()
print(" ")
print(f"Checking for mesh file: {mesh_filename}")
if os.path.exists(mesh_file):
print(f"Mesh file: {mesh_filename} found in folder")
else:
print('Mesh file not found')
for lines_in_output, line in enumerate(lines):
if target_string in line:
if lines_in_output + 1 < len(lines):
next_line = lines[lines_in_output + 1]
volume_mesh_elements = int(next_line.split(" ")[0])
print(f'Quantidade de volumes na malha: {volume_mesh_elements}')
else:
print("Error checking for the number of volume mesh elements")
break
else:
print("Number of volume mesh elements not found in the file.")
print(" ")
print(f"Checking file: {history_file}")
data_history = np.loadtxt(history_file, comments='"', delimiter=',')
# Case name differentiation
case_h = str(case_number)
casename = f'h{case_number}'
# Get data from history file
iter_data = data_history[:, 2]
rms_data = data_history[:, 3]
cd_data = data_history[:, 4]
csf_data = data_history[:, 5]
cl_data = data_history[:, 6]
# Determine the number of values for mean calculation
value_pool = len(iter_data) // 5
# Calculate mean values from the last fifth part of the values
cd_mean = np.mean(cd_data[-value_pool:])
cl_mean = np.mean(cl_data[-value_pool:])
csf_mean = np.mean(csf_data[-value_pool:])
# Calculate the standard deviation
cd_std = np.std(cd_data[-value_pool:])
cl_std = np.std(cl_data[-value_pool:])
csf_std = np.std(csf_data[-value_pool:])
# Determine the number of iterations made and to make
iter_made = np.max(iter_data)+1
iter_max = 15000
# Determine the progress percentage made
sim_prog = (iter_made/iter_max) * 100
if sim_prog > 100:
sim_prog = 100
# Defining the static loading bar function
def print_loading_bar(progress):
bar_width = 45
filled_width = int(bar_width * progress / 100)
remaining_width = bar_width - filled_width
loading_bar = '[' + '█' * filled_width + ' ' * remaining_width + ']'
print(loading_bar)
# Print Log
print('Iterations history file: history.csv found in folder')
print(f'{iter_made:.0f} iterations made')
print(f'{sim_prog:.2f}% done with the simulation based on expected {iter_max:.0f} iterations')
print_loading_bar(sim_prog)
print("")
print('Média:')
print(f'CD: {cd_mean:.5f}')
print(f'CL: {cl_mean:.5f}')
print(f'CSF: {csf_mean:.5f}')
print("")
print('Desvio Padrão:')
print(f'CD: {cd_std:.5f}')
print(f'CL: {cl_std:.5f}')
print(f'CSF: {csf_std:.5f}')
print("")
# Calculate the standard deviation as a percentage of the mean
cd_std_percent = np.abs((cd_std / cd_mean) * 100)
cl_std_percent = np.abs((cl_std / cl_mean) * 100)
csf_std_percent = np.abs((csf_std / csf_mean) * 100)
print('Desvio Padrão em formato percentual absoluto em relação à média:')
print(f'CD: {cd_std_percent:.2f}%')
print(f'CL: {cl_std_percent:.2f}%')
print(f'CSF: {csf_std_percent:.2f}%')
print("")
print("###################################################################")
print("")
# Find the index of the data point where the mean is calculated
mean_index = len(iter_data) - value_pool
#################################################
######### Plotting values #######################
#################################################
# Plotting CD and CL
fig, ax1 = plt.subplots()
# Plotting CD data
color_cd = 'tab:red'
ax1.set_xlabel('Iterações')
ax1.set_ylabel('CD', color=color_cd)
ax1.plot(iter_data, cd_data, color=color_cd)
ax1.tick_params(axis='y', labelcolor=color_cd)
# Centering the CD axis on zero
cd_max = np.max(np.abs(cd_data))
ax1.set_ylim(-cd_max, cd_max)
# Creating a second y-axis for CL data
ax2 = ax1.twinx()
# Plotting CL data
color_cl = 'tab:blue'
ax2.set_ylabel('CL', color=color_cl)
ax2.plot(iter_data, cl_data, color=color_cl)
ax2.tick_params(axis='y', labelcolor=color_cl)
# Centering the CL axis on zero
cl_max = np.max(np.abs(cl_data))
ax2.set_ylim(-cl_max, cl_max)
# Creating a third y-axis for CSF data
ax3 = ax1.twinx()
# Plotting CSF data
color_csf = 'tab:green'
ax3.spines['right'].set_position(('outward', 60)) # Adjust position of the third y-axis
ax3.set_ylabel('CSF', color=color_csf)
ax3.plot(iter_data, csf_data, color=color_csf)
ax3.tick_params(axis='y', labelcolor=color_csf)
# Centering the CSF axis on zero
csf_max = np.max(np.abs(csf_data)*30)
ax3.set_ylim(-csf_max, csf_max)
# Adding a legend
lines = [plt.Line2D([], [], color=color_cd, label='CD'),
plt.Line2D([], [], color=color_cl, label='CL'),
plt.Line2D([], [], color=color_csf, label='CSF')]
plt.legend(handles=lines, loc='upper left')
# Displaying the mean values in a box
mean_box_text = f'CD Médio: {cd_mean:.5f}\nCL Médio: {cl_mean:.5f}\nCSF Médio: {csf_mean:.5f}'
plt.text(0.98, 0.95, mean_box_text, transform=ax1.transAxes,
verticalalignment='top', horizontalalignment='right',
bbox=dict(facecolor='white', edgecolor='black', boxstyle='round,pad=0.3'))
# Adding a vertical line at the mean index
plt.axvline(x=iter_data[mean_index], color='grey', linestyle='-.')
plt.axvline(x=0, color='black', linestyle='-')
# Setting the title and subtitle with enlarged font size
plt.title('Evolução de CD, CL e CSF ao longo das iterações', fontsize=15)
plt.suptitle(f'Caso {casename}', y=0.95, fontsize=30, fontweight='bold')
# Show plot grid with vertical lines and bolden zero line
plt.grid(True, axis='both', which='major', linestyle='--', linewidth=0.5)
ax1.axhline(0, color='k', linewidth=1.5)
ax2.axhline(0, color='k', linewidth=1.5)
ax3.axhline(0, color='k', linewidth=1.5)
# Adjusting layout
plt.tight_layout(rect=[0, 0, 1.1, 1])
# Set the figure size
fig.set_size_inches(12, 5)
# Save the plot as a PNG file with casename in the file name
filename = f"convergence_CL_CD_CSF_{casename}.png"
#history_plotter_fig_plain_path = r'C:\Users\mathe\Documents\Meus Arquivos\UnB\Projeto de Pesquisa\Cluster Mirror\pg2\pg_files\results\History Plotter Figs\Plain'
#simulating_folder_name = r'Simulating'
if sim_prog >= 100:
save_fig_param = os.path.join(history_plotter_fig_plain_path, filename)
plt.savefig(save_fig_param, dpi=300)
else:
save_fig_param = os.path.join(history_plotter_fig_plain_path, simulating_folder_name, filename)
plt.savefig(save_fig_param, dpi=300)
# Displaying the plot
#plt.show()
plt.close()
#################################################
######### Full Technincal Plot ##################
#################################################
# Plotting CD and CL
fig, ax1 = plt.subplots()
# Plotting CD data
color_cd = 'tab:red'
ax1.set_xlabel('Iterações')
ax1.set_ylabel('CD', color=color_cd)
ax1.plot(iter_data, cd_data, color=color_cd)
ax1.tick_params(axis='y', labelcolor=color_cd)
# Centering the CD axis on zero
cd_max = np.max(np.abs(cd_data))
ax1.set_ylim(-cd_max, cd_max)
# Creating a second y-axis for CL data
ax2 = ax1.twinx()
# Plotting CL data
color_cl = 'tab:blue'
ax2.set_ylabel('CL', color=color_cl)
ax2.plot(iter_data, cl_data, color=color_cl)
ax2.tick_params(axis='y', labelcolor=color_cl)
# Centering the CL axis on zero
cl_max = np.max(np.abs(cl_data))
ax2.set_ylim(-cl_max, cl_max)
# Creating a third y-axis for CSF data
ax3 = ax1.twinx()
# Plotting CSF data
color_csf = 'tab:green'
ax3.spines['right'].set_position(('outward', 60)) # Adjust position of the third y-axis
ax3.set_ylabel('CSF', color=color_csf)
ax3.plot(iter_data, csf_data, color=color_csf)
ax3.tick_params(axis='y', labelcolor=color_csf)
# Centering the CSF axis on zero
csf_max = np.max(np.abs(csf_data)*30)
ax3.set_ylim(-csf_max, csf_max)
# Adding a legend
lines = [plt.Line2D([], [], color=color_cd, label='CD'),
plt.Line2D([], [], color=color_cl, label='CL'),
plt.Line2D([], [], color=color_csf, label='CSF')]
plt.legend(handles=lines, loc='upper left')
# Displaying the mean values in a box
mean_box_text = f'CD Médio: {cd_mean:.5f} ± {cd_std_percent:.2f}%\nCL Médio: {cl_mean:.5f} ± {cl_std_percent:.2f}%\nCSF Médio: {csf_mean:.5f} ± {csf_std_percent:.2f}%'
plt.text(0.98, 0.95, mean_box_text, transform=ax1.transAxes,
verticalalignment='top', horizontalalignment='right',
bbox=dict(facecolor='white', edgecolor='black', boxstyle='round,pad=0.3'))
# Adding a vertical line at the mean index
plt.axvline(x=iter_data[mean_index], color='grey', linestyle='-.')
plt.axvline(x=0, color='black', linestyle='-')
# Setting the title and subtitle with enlarged font size
if sim_prog >= 100:
plt.title(f'Evolução de CD, CL e CSF ao longo das iterações', fontsize=15)
else:
plt.title(f'Evolução de CD, CL e CSF ao longo de {sim_prog:.2f}% das iterações planejadas', fontsize=15)
plt.suptitle(f'Caso {casename}', y=0.95, fontsize=30, fontweight='bold')
# Show plot grid with vertical lines and bolden zero line
plt.grid(True, axis='both', which='major', linestyle='--', linewidth=0.5)
ax1.axhline(0, color='k', linewidth=1.5)
ax2.axhline(0, color='k', linewidth=1.5)
ax3.axhline(0, color='k', linewidth=1.5)
# Adjusting layout
plt.tight_layout(rect=[0, 0, 1.1, 1])
# Set the figure size
fig.set_size_inches(12, 5)
# Save the plot as a PNG file with casename in the file name
filename = f"convergence_full_CL_CD_CSF_{casename}.png"
if sim_prog >= 100:
save_fig_param = os.path.join(history_plotter_fig_full_path, filename)
plt.savefig(save_fig_param, dpi=300)
else:
save_fig_param = os.path.join(history_plotter_fig_full_path, simulating_folder_name, filename)
plt.savefig(save_fig_param, dpi=300)
# Displaying the plot
#plt.show()
plt.close()
#################################################
###### Update the csv results file ##############
#################################################
def update_csv_file(filename, h_input, cl_simulation, cd_simulation , q, s, g):
rows = []
with open(filename, 'r') as file:
reader = csv.reader(file)
rows = list(reader)
header = rows[0]
cl_simulation_index = header.index('*CL - Simulation*')
cd_simulation_index = header.index('*CD - Simulation*')
cl_zerihan_index = header.index('*CL - Zerihan*')
delta_cl_index = header.index('*Delta CL*')
cd_zerihan_index = header.index('*CD - Zerihan*')
delta_cd_index = header.index('*Delta CD*')
delta_fy_kgf_index = header.index('*Delta Fy (Kgf)*')
delta_fx_kgf_index = header.index('*Delta Fx (Kgf)*')
delta_fy_pct_index = header.index('*Delta Fy (%)*')
delta_fx_pct_index = header.index('*Delta Fx (%)*')
for row in rows[1:]:
h_value = float(row[0])
if h_value == float(h_input):
row[cl_simulation_index] = f'{cl_simulation:.5f}'
row[cd_simulation_index] = f'{cd_simulation:.5f}'
delta_cl = np.abs(cl_simulation) - np.abs(float(row[cl_zerihan_index]))
row[delta_cl_index] = f'{delta_cl:.5f}'
delta_cd = np.abs(cd_simulation) - np.abs(float(row[cd_zerihan_index]))
row[delta_cd_index] = f'{delta_cd:.5f}'
delta_fy_kgf = delta_cl * q * s / g
row[delta_fy_kgf_index] = f'{delta_fy_kgf:.5f}'
delta_fx_kgf = delta_cd * q * s / g
row[delta_fx_kgf_index] = f'{delta_fx_kgf:.5f}'
delta_fy_pct = (np.abs(delta_cl))/(np.max([np.abs(cl_simulation),np.abs(float(row[cl_zerihan_index]))]))
row[delta_fy_pct_index] = f'{delta_fy_pct:.5f}'
delta_fx_pct = (np.abs(delta_cd))/(np.max([np.abs(cd_simulation),np.abs(float(row[cd_zerihan_index]))]))
row[delta_fx_pct_index] = f'{delta_fx_pct:.5f}'
with open(filename, 'w', newline='') as file:
writer = csv.writer(file)
writer.writerows(rows)
# Updating the results .csv file:
results_filename = 'all_results.csv'
results_file = os.path.join(results_file_path, results_filename)
cl_simulation = cl_mean
cd_simulation = cd_mean
u_sim = 30 # m/s
rho = 1.2886 # kg/m^3
q = ((u_sim ** 2) * rho) / 2 # (u^2 * rho) / 2
s = 0.405 # m^2
g = 9.80665 # m/s^2
update_csv_file(results_file, case_h, cl_simulation, cd_simulation, q, s, g)
else:
if os.path.exists(mesh_file):
print(f"No history file found in folder {folder_name}.")
print("")
print('This probably means the simulation hasn\'t started yet, check the queue')
print("")
print("###################################################################")
print("")
else:
print(f"History file not found.")
print("")
print('This probably means the mesh file hast\'t been uploaded and the simulation hasn\'t started yet')
print("")
print("###################################################################")
print("")
if machine == 1:
end = input('Aperte enter pra sair')
else:
end = 'end program'
# Projeto de Graduação 2
# Matheus Ribeiro Vidal
# 17/06/2023
import numpy as np
import matplotlib.pyplot as plt
# Load data from the 'all_results.csv' file
data_results = np.loadtxt('all_results.csv', comments='*', delimiter=',')
# Extract the necessary data columns
h = data_results[:, 0]
h_c = h[:]/380
cl_zerihan = data_results[:, 2]
cd_zerihan = data_results[:, 3]
cl_simulation = data_results[:, 4] * -1
delta_cl = data_results[:, 5]
delta_fy_kgf = data_results[:, 6]
delta_fy_percent = data_results[:, 7] * 100
cd_simulation = data_results[:, 8]
delta_cd = data_results[:, 9]
delta_fx_kgf = data_results[:, 10]
delta_fx_percent = data_results[:, 11] * 100
# Filter out zero values of cl_simulation
nonzero_cl_indices = np.nonzero(cl_simulation)
h_c_nonzero = h_c[nonzero_cl_indices]
h_nonzero = h[nonzero_cl_indices]
cl_simulation_nonzero = cl_simulation[nonzero_cl_indices]
# Choosing figure sizes and figure folder path
fig_wid = 10
fig_hei = 12
folder_path = 'All Results Figs/'
################################################################################
###################### Plotting the Coefficient Values #########################
################################################################################
# Plot and compare the coefficient of lift (CL) data
print('CL')
for physics_cutoff_point in [10]:
plt.figure(figsize=(fig_wid, fig_hei))
plt.plot(h_c, cl_zerihan, 'bs', label='Experimental', markersize=3)
plt.plot(h_c, cl_zerihan, color='blue', linestyle='--', linewidth=0.7)
plt.plot(h_c_nonzero, cl_simulation_nonzero, 'ro', label='Simulação', markersize=3)
plt.plot(h_c_nonzero, cl_simulation_nonzero, color='red', linestyle='--', linewidth=0.7)
# Perform linear regression for up to the pyhsics cutoff point of experimental CL
coefficients_exp_cl_1 = np.polyfit(h_c[:physics_cutoff_point], cl_zerihan[:physics_cutoff_point], 1)
trendline_exp_cl_1 = np.polyval(coefficients_exp_cl_1, h_c[:physics_cutoff_point])
# Perform linear regression for up to the pyhsics cutoff point of experimental CL
coefficients_exp_cl_2 = np.polyfit(h_c[physics_cutoff_point:], cl_zerihan[physics_cutoff_point:], 1)
trendline_exp_cl_2 = np.polyval(coefficients_exp_cl_2, h_c[physics_cutoff_point:])
# Plot the two separate trendlines for experimental CL data
plt.plot(h_c[:physics_cutoff_point], trendline_exp_cl_1, '-.', linewidth=0.8, label='Trend (Experimental - Parte 1)', color='lightblue')
plt.plot(h_c[physics_cutoff_point:], trendline_exp_cl_2, '-.', linewidth=0.8, label='Trend (Experimental - Parte 2)', color='lightblue')
# Perform linear regression for up to the pyhsics cutoff point of simulation CL
coefficients_sim_cl_1 = np.polyfit(h_c_nonzero[:physics_cutoff_point], cl_simulation_nonzero[:physics_cutoff_point], 1)
trendline_sim_cl_1 = np.polyval(coefficients_sim_cl_1, h_c_nonzero[:physics_cutoff_point])
# Perform linear regression for up to the pyhsics cutoff point of simulation CL
coefficients_sim_cl_2 = np.polyfit(h_c_nonzero[physics_cutoff_point:], cl_simulation_nonzero[physics_cutoff_point:], 1)
trendline_sim_cl_2 = np.polyval(coefficients_sim_cl_2, h_c_nonzero[physics_cutoff_point:])
# Plot the two separate trendlines for simulation CL data
plt.plot(h_c_nonzero[:physics_cutoff_point], trendline_sim_cl_1, '-.', linewidth=0.8, label='Trend (Simulação - Parte 1)', color='lightcoral')
plt.plot(h_c_nonzero[physics_cutoff_point:], trendline_sim_cl_2, '-.', linewidth=0.8, label='Trend (Simulação - Parte 2)', color='lightcoral')
# Calculate the midpoint x-coordinate
midpoint_x = (h_c[physics_cutoff_point - 1] + h_c[physics_cutoff_point]) / 2.0
# Plot the vertical line at the midpoint
plt.axvline(x=midpoint_x, color='gray', linestyle='--', linewidth=0.9, label='Desaparecimento da Bolha de Recirculação')
plt.xlabel('h/c')
plt.ylabel('CL')
plt.xlim(0, 0.6)
plt.xticks(np.arange(0, 0.65, 0.05))
plt.ylim(1.6, 3.1)
plt.yticks(np.arange(1.6, 3.15, 0.05))
plt.title('Comparativo dos Resultados das Simulações com os Experimentos de Zerihan (2001)')
plt.suptitle('Coeficiente de Sustentação', y=0.95, fontsize=30, fontweight='bold')
plt.legend()
plt.grid(True, linestyle=':')
plt.savefig(folder_path + 'coefficient_of_lift.png')
print(f'Coeficiente linear dos dados experimentais para CL, na parte 1: {coefficients_exp_cl_1[0]}')
print(f'Coeficiente linear dos dados de siumalção para CL, na parte 1: {coefficients_sim_cl_1[0]}')
print(f'Grau de Paralelismo, Parte 1: {1 - np.abs(coefficients_sim_cl_1[0]-coefficients_exp_cl_1[0])/np.abs(coefficients_exp_cl_1[0])}')
print(f'Razão da diferença entre os coeficientes e o coeficiente dos dados experimentais, Parte 1: {np.abs(coefficients_sim_cl_1[0]-coefficients_exp_cl_1[0])/np.abs(coefficients_exp_cl_1[0])}')
print(f'Coeficiente linear dos dados experimentais para CL, na parte 2: {coefficients_exp_cl_2[0]}')
print(f'Coeficiente linear dos dados de siumlação para CL, na parte 2: {coefficients_sim_cl_2[0]}')
print(f'Grau de Paralelismo, Parte 2: {1 - np.abs(coefficients_sim_cl_2[0]-coefficients_exp_cl_2[0])/np.abs(coefficients_exp_cl_2[0])}')
print(f'Razão da diferença entre os coeficientes e o coeficiente dos dados experimentais, Parte 2: {np.abs(coefficients_sim_cl_2[0]-coefficients_exp_cl_2[0])/np.abs(coefficients_exp_cl_2[0])}')
# print(f'Grau de Paralelismo, Parte 2, {physics_cutoff_point}: {1 - np.abs(coefficients_sim_cl_2[0]-coefficients_exp_cl_2[0])/np.abs(coefficients_exp_cl_2[0])}')
# plt.show()
# Filter out zero values of cd_simulation
nonzero_cd_indices = np.nonzero(cd_simulation)
h_c_nonzero = h_c[nonzero_cd_indices]
cd_simulation_nonzero = cd_simulation[nonzero_cd_indices]
# Plot and compare the coefficient of drag (CD) data
print('CD')
for physics_cutoff_point in [10]:
plt.figure(figsize=(fig_wid, fig_hei))
plt.plot(h_c, cd_zerihan, 'bs', label='Experimental', markersize=3)
plt.plot(h_c, cd_zerihan, color='blue', linestyle='--', linewidth=0.7)
plt.plot(h_c_nonzero, cd_simulation_nonzero, 'ro', label='Simulação', markersize=3)
plt.plot(h_c_nonzero, cd_simulation_nonzero, color='red', linestyle='--', linewidth=0.7)
# Perform linear regression for up to the pyhsics cutoff point of experimental CD
coefficients_exp_cd_1 = np.polyfit(h_c[:physics_cutoff_point], cd_zerihan[:physics_cutoff_point], 1)
trendline_exp_cd_1 = np.polyval(coefficients_exp_cd_1, h_c[:physics_cutoff_point])
# Perform linear regression for after the pyhsics cutoff point of experimental CD
coefficients_exp_cd_2 = np.polyfit(h_c[physics_cutoff_point:], cd_zerihan[physics_cutoff_point:], 1)
trendline_exp_cd_2 = np.polyval(coefficients_exp_cd_2, h_c[physics_cutoff_point:])
# Plot the two separate trendlines for experimental CD data
plt.plot(h_c[:physics_cutoff_point], trendline_exp_cd_1, '-.', linewidth=0.8, label='Trend (Experimental - Parte 1)', color='lightblue')
plt.plot(h_c[physics_cutoff_point:], trendline_exp_cd_2, '-.', linewidth=0.8, label='Trend (Experimental - Parte 2)', color='lightblue')
# Perform linear regression for up to the pyhsics cutoff point of simulation CD
coefficients_sim_cd_1 = np.polyfit(h_c_nonzero[:physics_cutoff_point], cd_simulation_nonzero[:physics_cutoff_point], 1)
trendline_sim_cd_1 = np.polyval(coefficients_sim_cd_1, h_c_nonzero[:physics_cutoff_point])
# Perform linear regression for after the pyhsics cutoff point of simulation CD
coefficients_sim_cd_2 = np.polyfit(h_c_nonzero[physics_cutoff_point:], cd_simulation_nonzero[physics_cutoff_point:], 1)
trendline_sim_cd_2 = np.polyval(coefficients_sim_cd_2, h_c_nonzero[physics_cutoff_point:])
# Plot the two separate trendlines for simulation CD data
plt.plot(h_c_nonzero[:physics_cutoff_point], trendline_sim_cd_1, '-.', linewidth=0.8, label='Trend (Simulação - Parte 1)', color='lightcoral')
plt.plot(h_c_nonzero[physics_cutoff_point:], trendline_sim_cd_2, '-.', linewidth=0.8, label='Trend (Simulação - Parte 2)', color='lightcoral')
midpoint_x = (h_c[physics_cutoff_point - 1] + h_c[physics_cutoff_point]) / 2.0
# Plot the vertical line at the midpoint
plt.axvline(x=midpoint_x, color='gray', linestyle='--', linewidth=0.9, label='Desaparecimento da Bolha de Recirculação')
plt.xlabel('h/c')
plt.ylabel('CD')
plt.xlim(0, 0.6)
plt.xticks(np.arange(0, 0.65, 0.05))
plt.ylim(0.17, 0.32)
plt.yticks(np.arange(0.17, 0.33, 0.01))
plt.title('Comparativo dos Resultados das Simulações com os Experimentos de Zerihan (2001)')
plt.suptitle('Coeficiente de Arrasto', y=0.95, fontsize=30, fontweight='bold')
plt.legend()
plt.grid(True, linestyle=':')
plt.savefig(folder_path + 'coefficient_of_drag.png')
print(f'Coeficiente linear dos dados experimentais para CD, na parte 1: {coefficients_exp_cd_1[0]}')
print(f'Coeficiente linear dos dados de simulação para CD, na parte 1: {coefficients_sim_cd_1[0]}')
print(f'Grau de Paralelismo, Parte 1: {1 - np.abs(coefficients_sim_cd_1[0]-coefficients_exp_cd_1[0])/np.abs(coefficients_exp_cd_1[0])}')
print(f'Razão da diferença entre os coeficientes e o coeficiente dos dados experimentais, Parte 1: {np.abs(coefficients_sim_cd_1[0]-coefficients_exp_cd_1[0])/np.abs(coefficients_exp_cd_1[0])}')
print(f'Coeficiente linear dos dados experimentais para CD, na parte 2: {coefficients_exp_cd_2[0]}')
print(f'Coeficiente linear dos dados de simulação para CD, na parte 2: {coefficients_sim_cd_2[0]}')
print(f'Grau de Paralelismo, Parte 2: {1 - np.abs(coefficients_sim_cd_2[0]-coefficients_exp_cd_2[0])/np.abs(coefficients_exp_cd_2[0])}')
print(f'Razão da diferença entre os coeficientes e o coeficiente dos dados experimentais, Parte 2: {np.abs(coefficients_sim_cd_2[0]-coefficients_exp_cd_2[0])/np.abs(coefficients_exp_cd_2[0])}')
# plt.show()
################################################################################
###################### Plotting the Force Values ###############################
################################################################################
########## F in X Axis ############################################################
# Create a Boolean mask to filter out rows with delta_fx_percent equal to 100
mask = delta_fx_percent != 100
# Filter the data based on the mask
filtered_h_c = h_c[mask]
filtered_delta_fx_kgf = delta_fx_kgf[mask]
filtered_delta_fx_percent = delta_fx_percent[mask]
filtered_h = h[mask]
# Calculate the maximum absolute value of delta_fx_kgf
max_abs_fx_kgf = max(abs(filtered_delta_fx_kgf))
# Create a figure with two y-axes
fig, ax1 = plt.subplots(figsize=(fig_wid, fig_hei))
ax2 = ax1.twinx()
# Plot filtered_delta_fx_kgf on the first y-axis
line1 = ax1.plot(filtered_h_c, filtered_delta_fx_kgf, 'gv', label='\u0394Fx (kgf)', markersize=3)
line2 = ax1.plot(filtered_h_c, filtered_delta_fx_kgf, color='green', linestyle='--', linewidth=0.7)
ax1.set_xlabel('h/c')
ax1.set_ylabel('\u0394Fx (kgf)')
ax1.set_ylim(-max_abs_fx_kgf*1.1, max_abs_fx_kgf*1.1) # Set the y-axis limits centered around 0
ax1.set_xlim(0, 0.6)
ax1.set_xticks(np.arange(0, 0.65, 0.05))
ax1.grid(True, linestyle=':', linewidth=1, axis='x')
# Plot filtered_delta_fx_percent on the second y-axis
line3 = ax2.plot(filtered_h_c, filtered_delta_fx_percent, 'md', label='\u0394Fx (%)', markersize=3)
line4 = ax2.plot(filtered_h_c, filtered_delta_fx_percent, color='magenta', linestyle='--', linewidth=0.7)
ax2.set_ylabel('\u0394Fx (%)')
ax2.set_ylim(0, 100) # Set the y-axis limits from 0 to 100
ax2.set_yticks(np.arange(0, 101, 5))
ax2.grid(True, linestyle=':', linewidth=1)
# Get the minimum and maximum values for the y-axis data
min_val = np.min(np.abs(filtered_delta_fx_kgf))
max_val = np.max(np.abs(filtered_delta_fx_kgf))
min_val_percent = np.min(np.abs(filtered_delta_fx_percent))
max_val_percent = np.max(np.abs(filtered_delta_fx_percent))
min_index_fx = np.argmin(np.abs(filtered_delta_fx_percent))
max_index_fx = np.argmax(np.abs(filtered_delta_fx_percent))
min_h_fx = filtered_h[min_index_fx]
max_h_fx = filtered_h[max_index_fx]
# Create a text box with the minimum and maximum values
text_box = f'Min: {min_val:.3f} kgf ou {min_val_percent:.2f}% em h = {min_h_fx:.0f} mm\nMax: {max_val:.3f} kgf ou {max_val_percent:.2f}% em h = {max_h_fx:.0f} mm'
props = dict(boxstyle='round', facecolor='white', alpha=0.5)
ax1.text(0.985, 0.89, text_box, transform=ax1.transAxes, fontsize=10, verticalalignment='bottom', horizontalalignment='right', bbox=props)
# Combine the handles and labels from both axes
lines = line1 + line3
labels = [l.get_label() for l in lines]
# Set titles and legend
plt.suptitle('Comparativo dos Valores de \u0394Fx', y=0.95, fontsize=30, fontweight='bold')
plt.title('Diferença em Força Exercida no Eixo X Entre Simulações e os Experimentos de Zerihan (2001)')
plt.legend(lines, labels, loc='upper right')
# Save the figure
plt.savefig(folder_path + 'delta_fx.png')
# plt.show()
########## F in Y Axis ############################################################
# Create a Boolean mask to filter out rows with delta_fy_percent equal to 100
mask = delta_fy_percent != 100
# Filter the data based on the mask
filtered_h_c = h_c[mask]
filtered_delta_fy_kgf = delta_fy_kgf[mask]
filtered_delta_fy_percent = delta_fy_percent[mask]
filtered_h = h[mask]
# Calculate the maximum absolute value of delta_fy_kgf
max_abs_fy_kgf = max(abs(filtered_delta_fy_kgf))
# Create a figure with two y-axes
fig, ax1 = plt.subplots(figsize=(fig_wid, fig_hei))
ax2 = ax1.twinx()
# Plot filtered_delta_fy_kgf on the first y-axis
line1 = ax1.plot(filtered_h_c, filtered_delta_fy_kgf, 'gv', label='\u0394Fy (kgf)', markersize=3)
line2 = ax1.plot(filtered_h_c, filtered_delta_fy_kgf, color='green', linestyle='--', linewidth=0.7)
ax1.set_xlabel('h/c')
ax1.set_ylabel('\u0394Fy (kgf)')
ax1.set_ylim(-max_abs_fy_kgf*1.1, max_abs_fy_kgf*1.1) # Set the y-axis limits centered around 0
ax1.set_xlim(0, 0.6)
ax1.set_xticks(np.arange(0, 0.65, 0.05))
ax1.grid(True, linestyle=':', linewidth=1, axis='x')
# Plot filtered_delta_fy_percent on the second y-axis
line3 = ax2.plot(filtered_h_c, filtered_delta_fy_percent, 'md', label='\u0394Fy (%)', markersize=3)
line4 = ax2.plot(filtered_h_c, filtered_delta_fy_percent, color='magenta', linestyle='--', linewidth=0.7)
ax2.set_ylabel('\u0394Fy (%)')
ax2.set_ylim(0, 100) # Set the y-axis limits from 0 to 100
ax2.set_yticks(np.arange(0, 101, 5))
ax2.grid(True, linestyle=':', linewidth=1)
# Get the minimum and maximum values for the y-axis data
min_val = np.min(np.abs(filtered_delta_fy_kgf))
max_val = np.max(np.abs(filtered_delta_fy_kgf))
min_val_percent = np.min(np.abs(filtered_delta_fy_percent))
max_val_percent = np.max(np.abs(filtered_delta_fy_percent))
min_index_fy = np.argmin(np.abs(filtered_delta_fy_percent))
max_index_fy = np.argmax(np.abs(filtered_delta_fy_percent))
min_h_fy = filtered_h[min_index_fy]
max_h_fy = filtered_h[max_index_fy]
# Create a text box with the minimum and maximum values
text_box = f'Min: {min_val:.3f} kgf ou {min_val_percent:.2f}% em h = {min_h_fy:.0f} mm\nMax: {max_val:.3f} kgf ou {max_val_percent:.2f}% em h = {max_h_fy:.0f} mm'
props = dict(boxstyle='round', facecolor='white', alpha=0.5)
ax1.text(0.985, 0.89, text_box, transform=ax1.transAxes, fontsize=10, verticalalignment='bottom', horizontalalignment='right', bbox=props)
# Combine the handles and labels from both axes
lines = line1 + line3
labels = [l.get_label() for l in lines]
# Set titles and legend
plt.suptitle('Comparativo dos Valores de \u0394Fy', y=0.95, fontsize=30, fontweight='bold')
plt.title('Diferença em Força Exercida no Eixo Y Entre Simulações e os Experimentos de Zerihan (2001)')
plt.legend(lines, labels, loc='upper right')
# Save the figure
plt.savefig(folder_path + 'delta_fy.png')
# plt.show()
################################################################################
###################### Plotting all Values over h ##############################
################################################################################
# Plot and compare the coefficient of lift (CL) data with 'h' as the x-axis
plt.figure(figsize=(fig_wid, fig_hei))
plt.plot(h, cl_zerihan, 'bs', label='Experimental', markersize=3)
plt.plot(h, cl_zerihan, color='blue', linestyle='--', linewidth=0.7)
plt.plot(h_nonzero, cl_simulation_nonzero, 'ro', label='Simulação', markersize=3)
plt.plot(h_nonzero, cl_simulation_nonzero, color='red', linestyle='--', linewidth=0.7)
plt.xlabel('h')
plt.ylabel('CL')
plt.xlim(0, 230)
plt.xticks(np.arange(0,240,10))
plt.ylim(1.6, 3.1)
plt.yticks(np.arange(1.6,3.15,0.05))
plt.title('Comparativo dos Resultados das Simulações com os Experimentos de Zerihan (2001)')
plt.suptitle('Coeficiente de Sustentação', y=0.95, fontsize=30, fontweight='bold')
plt.legend()
plt.grid(True, linestyle=':')
plt.savefig(folder_path + 'coefficient_of_lift_h.png')
# Plot and compare the coefficient of drag (CD) data with 'h' as the x-axis
plt.figure(figsize=(fig_wid, fig_hei))
plt.plot(h, cd_zerihan, 'bs', label='Experimental', markersize=3)
plt.plot(h, cd_zerihan, color='blue', linestyle='--', linewidth=0.7)
plt.plot(h_nonzero, cd_simulation_nonzero, 'ro', label='Simulação', markersize=3)
plt.plot(h_nonzero, cd_simulation_nonzero, color='red', linestyle='--', linewidth=0.7)
plt.xlabel('h')
plt.ylabel('CD')
plt.xlim(0, 230)
plt.xticks(np.arange(0,240,10))
plt.ylim(0.17, 0.32)
plt.yticks(np.arange(0.17,0.33,0.01))
plt.title('Comparativo dos Resultados das Simulações com os Experimentos de Zerihan (2001)')
plt.suptitle('Coeficiente de Arrasto', y=0.95, fontsize=30, fontweight='bold')
plt.legend()
plt.grid(True, linestyle=':')
plt.savefig(folder_path + 'coefficient_of_drag_h.png')
########## F in X Axis ############################################################
# Create a Boolean mask to filter out rows with delta_fx_percent equal to 100
mask = delta_fx_percent != 100
# Filter the data based on the mask
filtered_h_c = h_c[mask]
filtered_delta_fx_kgf = delta_fx_kgf[mask]
filtered_delta_fx_percent = delta_fx_percent[mask]
filtered_h = h[mask]
# Calculate the maximum absolute value of delta_fx_kgf
max_abs_fx_kgf = max(abs(filtered_delta_fx_kgf))
# Create a figure with two y-axes
fig, ax1 = plt.subplots(figsize=(fig_wid, fig_hei))
ax2 = ax1.twinx()
# Plot filtered_delta_fx_kgf on the first y-axis
line1 = ax1.plot(filtered_h, filtered_delta_fx_kgf, 'gv', label='\u0394Fx (kgf)', markersize=3)
line2 = ax1.plot(filtered_h, filtered_delta_fx_kgf, color='green', linestyle='--', linewidth=0.7)
ax1.set_xlabel('h')
ax1.set_ylabel('\u0394Fx (kgf)')
ax1.set_ylim(-max_abs_fx_kgf*1.1, max_abs_fx_kgf*1.1) # Set the y-axis limits centered around 0
ax1.set_xlim(0, 230)
ax1.set_xticks(np.arange(0, 240, 10))
ax1.grid(True, linestyle=':', linewidth=1, axis='x')
# Plot filtered_delta_fx_percent on the second y-axis
line3 = ax2.plot(filtered_h, filtered_delta_fx_percent, 'md', label='\u0394Fx (%)', markersize=3)
line4 = ax2.plot(filtered_h, filtered_delta_fx_percent, color='magenta', linestyle='--', linewidth=0.7)
ax2.set_ylabel('\u0394Fx (%)')
ax2.set_ylim(0, 100) # Set the y-axis limits from 0 to 100
ax2.set_yticks(np.arange(0, 101, 5))
ax2.grid(True, linestyle=':', linewidth=1)
# Get the minimum and maximum values for the y-axis data
min_val = np.min(np.abs(filtered_delta_fx_kgf))
max_val = np.max(np.abs(filtered_delta_fx_kgf))
min_val_percent = np.min(np.abs(filtered_delta_fx_percent))
max_val_percent = np.max(np.abs(filtered_delta_fx_percent))
min_index_fx = np.argmin(np.abs(filtered_delta_fx_percent))
max_index_fx = np.argmax(np.abs(filtered_delta_fx_percent))
min_h_fx = filtered_h[min_index_fx]
max_h_fx = filtered_h[max_index_fx]
# Create a text box with the minimum and maximum values
text_box = f'Min: {min_val:.3f} kgf ou {min_val_percent:.2f}% em h = {min_h_fx:.0f} mm\nMax: {max_val:.3f} kgf ou {max_val_percent:.2f}% em h = {max_h_fx:.0f} mm'
props = dict(boxstyle='round', facecolor='white', alpha=0.5)
ax1.text(0.985, 0.89, text_box, transform=ax1.transAxes, fontsize=10, verticalalignment='bottom', horizontalalignment='right', bbox=props)
# Combine the handles and labels from both axes
lines = line1 + line3
labels = [l.get_label() for l in lines]
# Set titles and legend
plt.suptitle('Comparativo dos Valores de \u0394Fx', y=0.95, fontsize=30, fontweight='bold')
plt.title('Diferença em Força Exercida no Eixo X Entre Simulações e os Experimentos de Zerihan (2001)')
plt.legend(lines, labels, loc='upper right')
# Save the figure
plt.savefig(folder_path + 'delta_fx_h.png')
# plt.show()
########## F in Y Axis ############################################################
# Create a Boolean mask to filter out rows with delta_fy_percent equal to 100
mask = delta_fy_percent != 100
# Filter the data based on the mask
filtered_h_c = h_c[mask]
filtered_delta_fy_kgf = delta_fy_kgf[mask]
filtered_delta_fy_percent = delta_fy_percent[mask]
filtered_h = h[mask]
# Calculate the maximum absolute value of delta_fy_kgf
max_abs_fy_kgf = max(abs(filtered_delta_fy_kgf))
# Create a figure with two y-axes
fig, ax1 = plt.subplots(figsize=(fig_wid, fig_hei))
ax2 = ax1.twinx()
# Plot filtered_delta_fy_kgf on the first y-axis
line1 = ax1.plot(filtered_h, filtered_delta_fy_kgf, 'gv', label='\u0394Fy (kgf)', markersize=3)
line2 = ax1.plot(filtered_h, filtered_delta_fy_kgf, color='green', linestyle='--', linewidth=0.7)
ax1.set_xlabel('h')
ax1.set_ylabel('\u0394Fy (kgf)')
ax1.set_ylim(-max_abs_fy_kgf*1.1, max_abs_fy_kgf*1.1) # Set the y-axis limits centered around 0
ax1.set_xlim(0, 230)
ax1.set_xticks(np.arange(0, 240, 10))
ax1.grid(True, linestyle=':', linewidth=1, axis='x')
# Plot filtered_delta_fy_percent on the second y-axis
line3 = ax2.plot(filtered_h, filtered_delta_fy_percent, 'md', label='\u0394Fy (%)', markersize=3)
line4 = ax2.plot(filtered_h, filtered_delta_fy_percent, color='magenta', linestyle='--', linewidth=0.7)
ax2.set_ylabel('\u0394Fy (%)')
ax2.set_ylim(0, 100) # Set the y-axis limits from 0 to 100
ax2.set_yticks(np.arange(0, 101, 5))
ax2.grid(True, linestyle=':', linewidth=1)
# Get the minimum and maximum values for the y-axis data
min_val = np.min(np.abs(filtered_delta_fy_kgf))
max_val = np.max(np.abs(filtered_delta_fy_kgf))
min_val_percent = np.min(np.abs(filtered_delta_fy_percent))
max_val_percent = np.max(np.abs(filtered_delta_fy_percent))
min_index_fy = np.argmin(np.abs(filtered_delta_fy_percent))
max_index_fy = np.argmax(np.abs(filtered_delta_fy_percent))
min_h_fy = filtered_h[min_index_fy]
max_h_fy = filtered_h[max_index_fy]
# Create a text box with the minimum and maximum values
text_box = f'Min: {min_val:.3f} kgf ou {min_val_percent:.2f}% em h = {min_h_fy:.0f} mm\nMax: {max_val:.3f} kgf ou {max_val_percent:.2f}% em h = {max_h_fy:.0f} mm'
props = dict(boxstyle='round', facecolor='white', alpha=0.5)
ax1.text(0.985, 0.89, text_box, transform=ax1.transAxes, fontsize=10, verticalalignment='bottom', horizontalalignment='right', bbox=props)
# Combine the handles and labels from both axes
lines = line1 + line3
labels = [l.get_label() for l in lines]
# Set titles and legend
plt.suptitle('Comparativo dos Valores de \u0394Fy', y=0.95, fontsize=30, fontweight='bold')
plt.title('Diferença em Força Exercida no Eixo Y Entre Simulações e os Experimentos de Zerihan (2001)')
plt.legend(lines, labels, loc='upper right')
# Save the figure
plt.savefig(folder_path + 'delta_fy_h.png')
# plt.show()
################################################################################
###################### Plotting CL/CD over h/c ##################################
################################################################################
print('CL/CD')
# Calculate the CL/CD ratio for both simulation and experimental data
cl_cd_ratio_exp = cl_zerihan / cd_zerihan
cl_cd_ratio_sim = cl_simulation_nonzero / cd_simulation_nonzero
# Plot and compare the CL/CD ratio data
plt.figure(figsize=(fig_wid, fig_hei))
plt.plot(h_c, cl_cd_ratio_exp, 'bs', label='Experimental', markersize=3)
plt.plot(h_c, cl_cd_ratio_exp, color='blue', linestyle='--', linewidth=0.7)
plt.plot(h_c_nonzero, cl_cd_ratio_sim, 'ro', label='Simulação', markersize=3)
plt.plot(h_c_nonzero, cl_cd_ratio_sim, color='red', linestyle='--', linewidth=0.7)
# Calculate the midpoint x-coordinate
midpoint_x = (h_c[physics_cutoff_point - 1] + h_c[physics_cutoff_point]) / 2.0
# Plot the vertical line at the midpoint
plt.axvline(x=midpoint_x, color='gray', linestyle='--', linewidth=0.9, label='Desaparecimento da Bolha de Recirculação')
plt.xlabel('h/c')
plt.ylabel('CL/CD')
plt.xlim(0, 0.6)
plt.xticks(np.arange(0, 0.65, 0.05))
plt.ylim(5, 12)
plt.yticks(np.arange(5, 13, 1))
plt.title('Comparativo da Razão CL/CD entre Simulações e os Experimentos de Zerihan (2001)')
plt.suptitle('Razão CL/CD', y=0.95, fontsize=30, fontweight='bold')
plt.legend()
plt.grid(True, linestyle=':')
plt.savefig(folder_path + 'cl_cd_ratio.png')
# Print CL/CD datapoints for experimental data
print('Experimental CL/CD datapoints:')
for i in range(len(h)):
print(f'{h[i]}, {cl_cd_ratio_exp[i]}')
# Print CL/CD datapoints for simulation data
print('\nSimulation CL/CD datapoints:')
for i in range(len(h_nonzero)):
print(f'{h_nonzero[i]}, {cl_cd_ratio_sim[i]}')
print('')
print(f'Done plotting the results, check {folder_path}')